题目内容
 (2012•江西模拟)如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,设∠OCD=α,∠BAD=β.
(2012•江西模拟)如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,设∠OCD=α,∠BAD=β.(1)若α=50°,求β的值;
(2)试探究α与β之间的数量关系,并求出OE∥AB时α的值.
分析:(1)延长AO交CD于F,利用已知条件和平行四边形的性质可证明:∠OCD=∠ODC,∠OAD=∠ODA,进一步得到∠COF=∠DOF=40°,再利用圆周角定理可得∠BAD=β=90°+20°=110°;
(2)α与β之间的数量关系为:β+
α=135°,连接OE,由?ABCD可知∠BCD=∠BAD=β,∠B+∠BAD=180°,所以∠BCD=∠OCE+α=β,即β=180°-β+α,整理得:2β=180°+α,再利用已知关系式求出OE∥AB时α的值即可.
(2)α与β之间的数量关系为:β+
| 1 |
| 2 |
解答:解:(1)延长AO交CD于F,
∵AB与⊙O相切于点A,
∴OA⊥AB,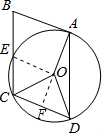
由?ABCD可知AB∥CD,
∴AF⊥CD,
而OC=OD=OA,
∴∠OCD=∠ODC,∠OAD=∠ODA,
∵∠OCD=α=50°,
∴∠COF=∠DOF=40°,
∴∠OAD=∠ODA=20°,
即∠BAD=β=90°+20°=110°;
(2)α与β之间的数量关系为:β+
α=135°,
连接OE,
∵∠OCD=∠ODC,OF⊥CD,
∴∠COF=∠DOF=90°-α,
∵∠OAD=∠ODA,
∴∠OAD=
(90°-α),
∴β=90°+
(90°-α)=135°-
α,
∵OE=OC,
∴∠OEC=∠OCE,
故当OE∥AB时,∠B=∠OCE,
由?ABCD可知∠BCD=∠BAD=β,∠B+∠BAD=180°,
∴∠BCD=∠OCE+α=β,即β=180°-β+α,2β=180°+α,
再由β=135°-
α,可求得α=45°.
故所求α=45°.
∵AB与⊙O相切于点A,
∴OA⊥AB,

由?ABCD可知AB∥CD,
∴AF⊥CD,
而OC=OD=OA,
∴∠OCD=∠ODC,∠OAD=∠ODA,
∵∠OCD=α=50°,
∴∠COF=∠DOF=40°,
∴∠OAD=∠ODA=20°,
即∠BAD=β=90°+20°=110°;
(2)α与β之间的数量关系为:β+
| 1 |
| 2 |
连接OE,
∵∠OCD=∠ODC,OF⊥CD,
∴∠COF=∠DOF=90°-α,
∵∠OAD=∠ODA,
∴∠OAD=
| 1 |
| 2 |
∴β=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∵OE=OC,
∴∠OEC=∠OCE,
故当OE∥AB时,∠B=∠OCE,
由?ABCD可知∠BCD=∠BAD=β,∠B+∠BAD=180°,
∴∠BCD=∠OCE+α=β,即β=180°-β+α,2β=180°+α,
再由β=135°-
| 1 |
| 2 |
故所求α=45°.
点评:本题考查了平行四边形的性质、圆的切线的性质、圆周角定理以及等腰三角形的判定和性质,还考查了学生的探究的能力,题目的难度不小.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 (2012•江西模拟)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为
(2012•江西模拟)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为