题目内容
有一个圆柱体礼盒，高9πcm，底面半径为2cm．现准备在礼盒表面粘贴彩带作为装饰，若彩带一端粘在A处，另一端绕礼盒侧面3周后粘帖在B处（AB在同一条母线上），则彩带最短为 cm．
15
本题考查了勾股定理和平面展开﹣最短路线问题，画出展开后的图形，根据两点之间线段最短，得出AD，由勾股定理求出线段AD，再代入3AD求出即可．
解：展开后图形如下图：
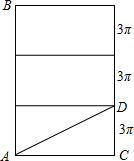
AC=2×2=4，
∵在Rt△ACD中，CD=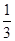
×9π=3，由勾股定理得：AD=5，
∴彩带最短是3×5=15，
故答案为：15．
解：展开后图形如下图：
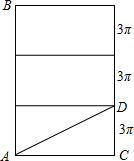
AC=2
×2=4，∵在Rt△ACD中，CD=
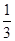×9π=3，由勾股定理得：AD=5，∴彩带最短是3×5
=15，故答案为：15
．
练习册系列答案
阅读快车系列答案
相关题目
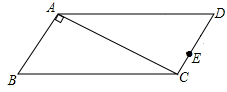
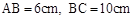，E是CD上的点，
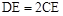．点P从D点出发，以1cm/s的速度沿DA运动至A点停止．则当△EDP为等腰三角形时，点P的运动时间为 ．
