Question

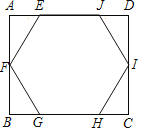
【题目】如图，在矩形ABCD中有一个正六边形EFGHIJ，其顶点均在矩形的边上，边EJ和边GH分别在矩形的边AD和BC上，则＝_____．

Answer 1

【答案】

【解析】

由正六边形和矩形的性质得出∠FEJ=120°，EJ=EF，∠A=90°，得出∠AEF=60°，∠AFE=30°，由直角三角形的性质得出EF=2AE，AF=AE，由题意得：AB=2AF=2AE，AD=2AE+EJ=4AE，即可得出结果．

∵六边形EFGHIJ是正六边形，四边形ABCD是矩形，

∴∠FEJ＝120°，EJ＝EF，∠A＝90°，

∴∠AEF＝60°，∠AFE＝30°，

∴EF＝2AE，AF＝AE，

由题意得：AB＝2AF＝2AE，AD＝2AE+EJ＝4AE，

∴；

故答案为．