题目内容
【题目】（1）如图①，在△ABC中，∠B=40°，∠C=80°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数；
（2）将（1）中“∠B=40°，∠C=80°”改为“∠B=x°，∠C=y°，∠C＞∠B”，
①其他条件不变，你能用含x，y的代数式表示∠EAD吗？请写出，并说明理由；
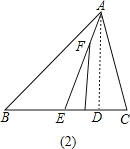
②如图②，AE平分∠BAC，F为AE上一点，FM⊥BC于点M，用含x，y的代数式表示∠EFM，并说明理由.
【答案】（1）∠EAD=20°；（2）①∠EAD=
y-x，理由见解析；②∠EFM=y-x，理由见解析．
【解析】试题分析：（1）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出即可；
（2）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出即可；
（3）根据三角形内角和定理求出∠BAC，求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠EAD=∠CAE-∠CAD求出∠EAD，推出∠FEM=∠EAD，即可得出答案．
试题解析：（1）∵∠B=40°，∠C=80°，
∴∠BAC=180°-∠B-∠C=60°，
∵AE平分∠BAC，
∴∠CAE=∠BAC=30°，
∵AD⊥BC，
∴∠ADC=90°，
∵∠C=80°，
∴∠CAD=90°-∠C=10°，
∴∠EAD=∠CAE-∠CAD=30°-10°=20°；
（2）∵三角形的内角和等于180°，
∴∠BAC=180°-∠B-∠C=180°-x-y，
∵AE平分∠BAC，
∴∠CAE= ∠BAC= (180°xy），
∵AD⊥BC，
∴∠ADC=90°，
∴∠CAD=90°-y，
∴∠EAD=∠CAE-∠CAD= （180°-x-y）-（90°-y）=y-x；
（3）过A作AD⊥BC于D，
∵三角形的内角和等于180°，
∴∠BAC=180°-∠B-∠C，
∵AE平分∠BAC，
∴∠CAE= ∠BAC= (180°x-y），
∵AD⊥BC，
∴∠ADC=90°，
∴∠CAD=90°-y，
∴∠EAD=∠CAE-∠CAD= （180°-x-y）-（90°-y）= y-x，
∵AD⊥BC，FM⊥BC，
∴AD∥FM，
∴∠EFM=∠EAD，
∴∠EFM= y-x．
