题目内容
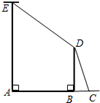
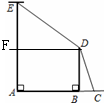
如图,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起拉线。已知公路的宽AB为8米,电线杆AE的高为12米,水泥撑杆BD高为6米,拉线CD与水平线AC的夹角为67.4°.求拉线CDE的总长l(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计)。(参考数据:sin67.4°≈ ,cos67.4°≈
,cos67.4°≈ ,,tan67.4°≈
,,tan67.4°≈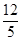 )
)
 ,cos67.4°≈
,cos67.4°≈ ,,tan67.4°≈
,,tan67.4°≈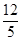 )
)
16.5m
试题分析:在Rt△DBC中,先根据∠DCB的正弦函数求得CD的长,
 ,根据矩形的性质可得DF=AB=8,
,根据矩形的性质可得DF=AB=8,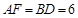 ,则可得到EF的长,再根据勾股定理求得ED的长,从而可以求得结果.
,则可得到EF的长,再根据勾股定理求得ED的长,从而可以求得结果.在Rt△DBC中,sin∠DCB=
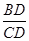 ,
,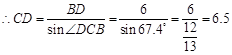 (m)
(m)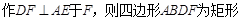
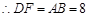 ,
,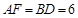 ,EF=AE-AF=12-6=6
,EF=AE-AF=12-6=6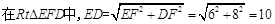 (m)
(m)l=10+6.5=16.5(m)
答:拉线CDE的总长l为16.5m.
点评:解直角三角形的应用是中考必考题,一半难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
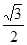 ,AB=8cm,AC=5cm,则△ABC的面积= cm2.
,AB=8cm,AC=5cm,则△ABC的面积= cm2.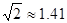 ,
,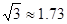 ,最后结果精确到1米)
,最后结果精确到1米)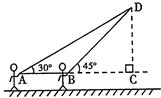
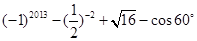 .
.
 .
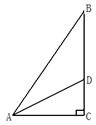
. 的直角三角板测量树高,已知小聪和树都与地面垂直,且相距
的直角三角板测量树高,已知小聪和树都与地面垂直,且相距 米,小聪身高AB为1.7米,则这棵树的高度= 米
米,小聪身高AB为1.7米,则这棵树的高度= 米
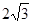 。
。
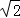 cos45°= .
cos45°= .