题目内容
【题目】长为![]() 的春游队伍,以
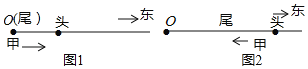
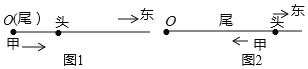
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() ,此时队伍在此过程中行进的路程为
,此时队伍在此过程中行进的路程为![]() .
.
【解析】
(1)①排头与O的距离为S头(m).等于排头行走的路程+队伍的长300,而排头行进的时间也是t(s),速度是2m/s,可以求出S头与t的函数关系式;
②甲赶到排头位置的时间可以根据追及问题的数量关系得出,代入求S即可;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m)是在S的基础上减少甲返回的路程,而甲返回的时间=总时间t-甲从排尾赶到排头的时间,于是可以求S甲与t的函数关系式;
(2)甲这次往返队伍的总时间为T(s),是甲从排尾追到排头用的时间与从排头返回排尾用时的和,可以根据追及问题和相遇问题的数量关系得出结果;在甲这次往返队伍的过程中队伍行进的路程=队伍速度×返回时间.
(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),∴S头=2t+300;
②甲从排尾赶到排头的时间为300÷(2v﹣v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m,甲返回时间为:(t﹣150)s,∴S甲=S头﹣S甲回=2×150+300﹣4(t﹣150)=﹣4t+1200;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S的值为600m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=﹣4t+1200.
(2)T=t追及+t返回![]() ,在甲这次往返队伍的过程中队伍行进的路程为:v
,在甲这次往返队伍的过程中队伍行进的路程为:v![]() 400;
400;
因此T与v的函数关系式为:T![]() ,此时队伍在此过程中行进的路程为400m.
,此时队伍在此过程中行进的路程为400m.

 口算能手系列答案
口算能手系列答案