题目内容
【题目】在平面直角坐标系中，如图1，抛物线y＝ax2+bx+c的对称轴为
，与x轴的交点A（﹣1，0）与y轴交于点C（0，﹣2）．
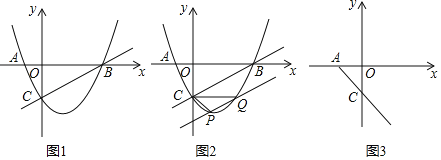
（1）求抛物线的解析式；
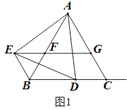
（2）如图2．点P是直线BC下方抛物线上的一点，过点P作BC的平行线交抛物线于点Q（点Q在点P右侧），连结BQ，当△PCQ的面积为△BCQ面积的一半时，求P点的坐标；
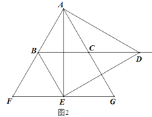
（3）现将该抛物线沿射线AC的方向进行平移，平移后的抛物线与直线AC的交点为A'、C'（点C'在点A'的下方），与x轴的交点为B'，当△AB'C'与△AA'B'相似时，求出点A′的横坐标．
【答案】（1）
；（2）点P（1，﹣3）；（3）点A′的横坐标为
．
【解析】
（1）由对称性可知B（4，0），设抛物线解析式为y＝a（x+1）（x﹣4），由待定系数法可求得抛物线的解析式；
（2）由平行线间距离处处相等可知，当△PCQ的面积为△BCQ面积的一半时，可求相关线段的长，再求得BC的解析式，将其与抛物线解析式联立可解；
（3）由平移的相关知识，结合图形分析，得出方程组，从而得解．
解：（1）由对称性可知B（4，0）
设抛物线解析式为y＝a（x+1）（x﹣4）
将（0，﹣2）代入得a＝
∴y＝x2﹣
x﹣2．
（2）由平行线间距离处处相等可知，当△PCQ的面积为△BCQ面积的一半时，PQ＝BC
∵C（0，﹣2），B（4，0）
∴BC＝
∴PQ＝
∴PQ2＝
＝5
∵直线BC的解析式为y＝x﹣2，PQ∥BC
∴设直线PQ的解析式为y＝x+b
则yP＝xP+b，yQ＝y＝xQ+b
联立
得
x2﹣4x﹣4﹣2b＝0
则xP+xQ＝4
∵PQ2＝＝5
∴
＝5，xQ﹣xP＝2
∴点P（1，﹣3）
（3）由点A（﹣1，0），C（0，﹣2）得直线AC的解析式为y＝﹣2x﹣2
设点A'坐标为（a，﹣2a﹣2），由平移的性质，可知AC＝A'C'＝
平移距离为AA'＝（a+1）
∴AC'（a+2）
当△AB'C'与△AA'B'相似时，只有当△AB'C'∽△AA'B'
∴AB'2＝AA'×AC'＝5（a+1）（a+2）
过点B'作AA'的平行线，交原抛物线于点D，连接AD，
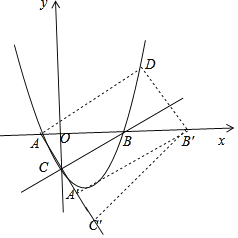
由平移知四边形ADB'A'为平行四边形，点D的纵坐标为2a+2
设点D的横坐标为m，则点B'坐标为（m+a+1，0）
∴AB'2＝（m+a+2）2＝5（a+1）（a+2），①
将点D（m，2a+2）代入y＝ x2﹣x﹣2得
﹣
﹣2＝2a+2，②
联立①②，解得：a＝
，
m2﹣9m+15＝0，
∴m＝
，或m＝
（舍）
∴a═＝
∴点A′的横坐标为
．
