��Ŀ����
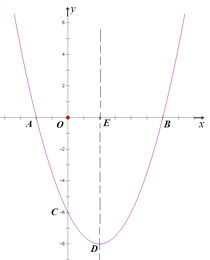
����Ŀ����ͼ��������y=ax2+bx��A����4��0����B����1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��
��1���������ߵĺ�������ʽ��
��2��д����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ��x����·�������ABP�����Ϊ15ʱ�������P�����ꣻ
��4������M��ֱ��BH���˶�����N��x�����˶������Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ����ֱ��д����ʱ��N�����꣮
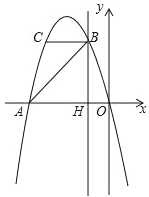 ��������
��������
���𰸡���1��y=��x2��4x����2��3����3����P����Ϊ����6����12����1����5������4��N������Ϊ��2��0����4��0����2��0����4��0����
��������������
��1������A��B���������y=ax2+bx���г�����a��b�ķ����飬�ⷽ�������a��b��ֵ���ɵõ������ߵĽ���ʽy=��x2��4x��
��2������1���������ߵĽ���ʽ��Ϊ������ʽ���õ������ߵĶԳ��ᣬ��ϵ�B�����꼴����õ�C�����꣬������A��B��C��������꼴�����S��ABC��ֵ��
��3������ͼ1������P��PF��ֱx�ᣬ��ֱ��AB�ڵ�F������A��B���������ֱ��AB�Ľ���ʽy=x+4�����P�ĺ�����Ϊm������P������Ϊ��m����m2��4m������F������Ϊ��m��m+4�����ɴ˿ɵ�PF= m2+5m+4��Ȼ����S��PAB=S��PFB-S��PFA=15�ɵ���![]() ����m2+5m+4����[(-1-m)-(-4-m)]=15����˷������m��ֵ���ɵõ���P�����ꣻ
����m2+5m+4����[(-1-m)-(-4-m)]=15����˷������m��ֵ���ɵõ���P�����ꣻ
��4�����Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ���ֵ�C��M��N�ֱ�Ϊֱ�Ƕ�����������������ۣ�I����MΪֱ�Ƕ��㣬��M��x���Ϸ�����MΪֱ�Ƕ�������M��x����·���II����NΪֱ�Ƕ�������N��y����Ҳࣻ��NΪֱ�Ƕ�������N��y�����ࣻIII��CΪֱ�Ƕ��㣻�����������������Ӧ��ͼ�Σ��ٽ����֪�������з������.
��⣺
��1���ѵ�A����4��0����B����1��3������������y=ax2+bx�У�
��![]() �����
�����![]() ��
��
�������߱���ʽΪy=��x2��4x��
��2����y=��x2+4x=����x+2��2+4��
�������߶Գ���Ϊx=��2��
����C�͵�B���ڶԳ���Գƣ���B������Ϊ����1��3����
��C����3��3����
��BC=2��
��S��ABC=![]() ��2��3=3��
��2��3=3��
��3����ͼ1����P����PF��ֱx�ᣬ��ֱ��AB�ڵ�F��
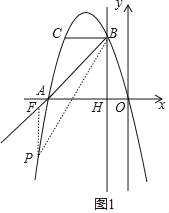
��A����4��0����B����1��3����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��AB�Ľ���ʽΪy=x+4��
���P��m����m2��4m������F��m��m+4����
��PF=m+4+m2+4m=m2+5m+4��
��S��PAB=![]() ����m2+5m+4����3=15��
����m2+5m+4����3=15��
m2+5m��6=0��
���m1=��6��m2=1��
����P��������6����12����1����5����
��4���Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ��������������ۣ�
���Ե�MΪֱ�Ƕ�����M��x���Ϸ�ʱ����ͼ2��CM=MN����CMN=90�㣬
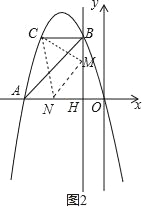
����CBM�ա�MHN��
��BC=MH=2��BM=HN=3��2=1��
��ON=OH+NH=2��
��N����2��0����
���Ե�MΪֱ�Ƕ�����M��x���·�ʱ����ͼ3��

�������ߣ�������ͼ��ʾ����ֱ�������Σ�Rt��NEM��Rt��MDC��
��Rt��NEM��Rt��MDC��
��EM=CD=5��
��OH=1��
��ON=NH��OH=5��1=4��
��N��4��0����
���Ե�NΪֱ�Ƕ�����N��y���Ҳ�ʱ����ͼ4��CN=MN����MNC=90�����������ߣ�
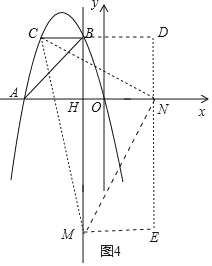
ͬ����Rt��NEM��Rt��MDC��
��ME=NH=DN=3��
��ON=3��1=2��
��N��2��0����
���Ե�NΪֱ�Ƕ�����N��y�����ʱ���������ߣ���ͼ5��
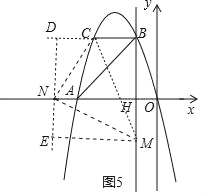
ͬ����ME=DN=NH=3��
��ON=1+3=4��
��N����4��0����
����CΪֱ�Ƕ���ʱ�����ڵ�C��-3��3����x��ľ���͵������߶Գ���x=-2�ľ��벻��ȣ����Դ�ʱ���ܹ������������ĵ���ֱ�������Σ�
���Ͽ�֪����CMNΪ����ֱ��������ʱN������Ϊ��2��0����4��0����2��0����4��0����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�