题目内容
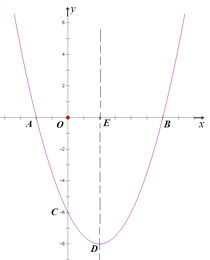
【题目】(题文)如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
【答案】(1) ![]() ,点D的坐标为(2,-8) (2) 点F的坐标为(7,
,点D的坐标为(2,-8) (2) 点F的坐标为(7,![]() )或(5,
)或(5,![]() )(3) 菱形对角线MN的长为
)(3) 菱形对角线MN的长为![]() 或
或![]() .
.
【解析】分析:(1)利用待定系数法,列方程求二次函数解析式.(2)利用解析法,∠FAB=∠EDB, tan∠FAG=tan∠BDE,求出F点坐标.(3)分类讨论,当MN在x轴上方时,在x轴下方时分别计算MN.
详解:
(1)∵OB=OC=6,
∴B(6,0),C(0,-6).
∴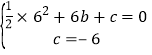 ,
,
解得![]() ,
,
∴抛物线的解析式为![]() .
.
∵![]() =
=![]() ,
,
∴点D的坐标为(2,-8).
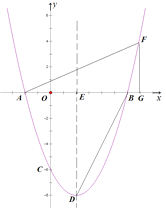
(2)如图,当点F在x轴上方时,设点F的坐标为(x,![]() ).过点F作FG⊥x轴于点G,易求得OA=2,则AG=x+2,FG=
).过点F作FG⊥x轴于点G,易求得OA=2,则AG=x+2,FG=![]() .
.
∵∠FAB=∠EDB,
∴tan∠FAG=tan∠BDE,
即![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).
当x=7时,y=![]() ,
,
∴点F的坐标为(7,![]() ).
).
当点F在x轴下方时,设同理求得点F的坐标为(5,![]() ).
).
综上所述,点F的坐标为(7,![]() )或(5,
)或(5,![]() ).
).
(3)∵点P在x轴上,
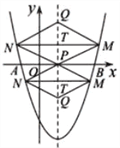
∴根据菱形的对称性可知点P的坐标为(2,0).
如图,当MN在x轴上方时,设T为菱形对角线的交点.
∵PQ=![]() MN,
MN,
∴MT=2PT.
设TP=n,则MT=2n. ∴M(2+2n,n).
∵点M在抛物线上,
∴![]() ,即
,即![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).
∴MN=2MT=4n=![]() .
.
当MN在x轴下方时,设TP=n,得M(2+2n,-n).
∵点M在抛物线上,
∴![]() ,
,
即![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).
∴MN=2MT=4n=![]() .
.
综上所述,菱形对角线MN的长为![]() 或
或![]() .
.

【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?