题目内容
【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,连接AF、CE.
(1)求证:△BFO≌△DEO;
(2)若AF⊥BC,试判断四边形AFCE的形状,并加以证明;
(3)若在(2)的条件下再添加EF平分∠AEC,试判断四边形AFCE的形状,无需说明理由.

【答案】(1)详见解析;
(2)四边形AFCE是矩形,证明见解析;
(3)四边形AFCE是正方形.
【解析】
(1)由平行四边形的性质得出OB=OD,OA=OC,AD∥BC,得出∠OBF=∠ODE,由ASA证明△BFO≌△DEO即可;
(2)由全等三角形的性质得出BF=DE,证出四边形AFCE是平行四边形,再证出∠AFC=90°,即可得出四边形AFCE是矩形.
(3)由EF平分∠AEC知∠AEF=∠CEF,再由AD∥BC知∠AEF=∠CFE,从而得∠CEF=∠CFE,继而知CE=CF,据此可得答案.
解:(1)∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,AD=BC,
∴∠OBF=∠ODE,
在△BFO和△DEO中,
∵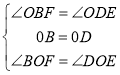 ,
,
∴△BFO≌△DEO(ASA);
(2)四边形AFCE是矩形;理由如下:
∵△BFO≌△DEO,
∴BF=DE,
∴CF=AE,
∵AD∥BC,
∴四边形AFCE是平行四边形;
又∵AF⊥BC,
∴∠AFC=90°,
∴四边形AFCE是矩形;
(3)∵EF平分∠AEC,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴四边形AFCE是正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了丰富老年人的晚年生活,甲、乙两单位准备组织退休职工到某风景区游玩.甲、乙两单位退休职工共![]() 人,其中乙单位人数少于
人,其中乙单位人数少于![]() 人,且甲单位人数不够
人,且甲单位人数不够![]() 人.经了解,该风景区的门票价格如下表:
人.经了解,该风景区的门票价格如下表:
数量(张) |
|
|
|
单价(元/张) |
|
|
|
如果两单位分别单独购买门票,一共应付![]() 元.
元.
(1)甲、乙两单位各有多少名退休职工准备参加游玩?
(2)如果甲单位有![]() 名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?