题目内容
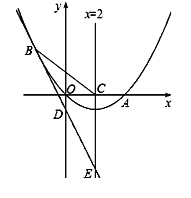
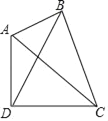
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.
(1)若BD=BC,证明:sin∠BCD=![]() .
.
(2)若AB=BC=4,AD+CD=6,求![]() 的值.
的值.
(3)若BD=CD,AB=6,BC=8,求sin∠BCD的值.
(注:本题可根据需要自己画图并解答)
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:
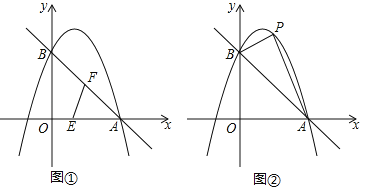
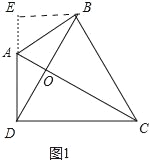
(1)如图1,过点B作BE⊥AD交AD的延长线于点E,由已知条件易得点A、B、C、D四点共圆,由此可得∠EAB=∠BCD,∠EDB=∠BCA,结合∠DEB=∠ABC=90°,可得△BED∽△ABC,从而可得sin∠BCD=sin∠EAB=![]() ,结合BD=BC即可得到所求结论;
,结合BD=BC即可得到所求结论;
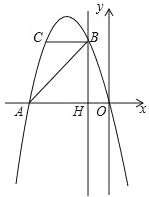
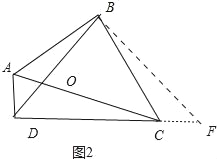
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.由已知条件通过证△DAB≌△CBF得到BD=BF,AD=CF,从而可得△DBF是等腰直角三角形,由此可得BD=![]() DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得
DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得![]() 的值;
的值;
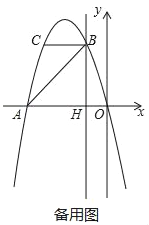
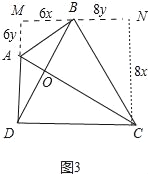
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,易得四边形DCNM是矩形,△ABM∽△BCN,从而可得![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=
,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=![]() =6
=6![]() y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=
y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=![]() 求得sin∠BCD的值了.
求得sin∠BCD的值了.
详解:
(1)如图1中,过点B作AD的垂线BE交DA的延长线于点E,
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴点A、B、C、D四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴![]() ,
,
∵ ∠EAB=∠BCD,sin∠EAB=![]() ,
,
∴sin∠BCD=![]() ;
;
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD=![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3![]() ,AC=
,AC=![]() ,
,
∴![]() .
.
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,则四边形DCNM是矩形,△ABM∽△BCN,
∴![]() ,
,
设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD=![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△ABM中,AB=![]() =6
=6![]() y,
y,
∴sin∠BCD=sin∠MAB=![]() .
.

【题目】某超市在“十一”长假期间对顾客实行优惠,规定如下:
一次性购物金额 | 优惠办法 |
不超过100元 | 不予优惠 |
超过100元但不超过500元 | 超过100元部分给予九折优惠 |
超过500元 | 超过500元部分给予八折优惠 |
(1)小明的爷爷一次性购200元的保健食品,他实际付款_____元;小明妈妈一次性购300元的衣服,她实际付款_____元;如果他们两人合作付款,则能少付_____元;
(2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她实际付款_____元;(用含x的式子表示,写最简结果)
(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(![]() ),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)