题目内容
如图,在⊙O中,直径AB与弦CD垂直,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线F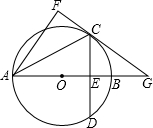 C与直线AB相交于点G.
C与直线AB相交于点G.(1)证明:直线FC与⊙O相切;
(2)若OB=BG,求证:四边形OCBD是菱形.
分析:(1)如图,连接OC,首先可以由OA=OC得到∠1=∠2,根据翻折可以得到∠2=∠3,由此即可证明直线FC与⊙O相切;
(2)由于OB=BG,由直径AB垂直弦CD可以得到CB=BD,而OB=OC=OD,由此可以得到OB=OC=OD=BD,然后即可证明题目的结论.
(2)由于OB=BG,由直径AB垂直弦CD可以得到CB=BD,而OB=OC=OD,由此可以得到OB=OC=OD=BD,然后即可证明题目的结论.
解答: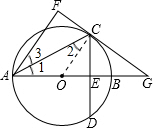 证明:(1)连接OC,
证明:(1)连接OC,
∵OA=OC,∴∠1=∠2
由翻折得,∠1=∠3,∠F=∠AEC=90°.
∴∠2=∠3.
∴OC∥AF.∴∠OCG=∠F=90°.
∵点C在圆上
∴直线FC与⊙O相切.
(2)证法一:
在Rt△OCG中,∵OB=BG,∴BC=
OG=OB,
∵直径AB垂直弦CD,∴
=
∴CB=BD,∵OB=OC=OD
∴BC=OC=OD=BD
∴四边形OCBD是菱形.
证法二:在Rt△OCG中,
∵OB=BG
∴BC=
OG=OB,
∵OB=OC,
∴CB=CO
∵AB垂直于弦CD,
∴OE=EB
∵直径AB垂直弦CD,
∴CE=ED
∴四边形OCBD是平行四边形,
∵AB垂直于弦CD,
∴四边形OCBD是菱形.
 证明:(1)连接OC,
证明:(1)连接OC,∵OA=OC,∴∠1=∠2
由翻折得,∠1=∠3,∠F=∠AEC=90°.
∴∠2=∠3.
∴OC∥AF.∴∠OCG=∠F=90°.
∵点C在圆上
∴直线FC与⊙O相切.
(2)证法一:
在Rt△OCG中,∵OB=BG,∴BC=
| 1 |
| 2 |
∵直径AB垂直弦CD,∴
 |
| CB |
 |
| BD |
∴CB=BD,∵OB=OC=OD
∴BC=OC=OD=BD
∴四边形OCBD是菱形.
证法二:在Rt△OCG中,
∵OB=BG
∴BC=
| 1 |
| 2 |
∵OB=OC,
∴CB=CO
∵AB垂直于弦CD,
∴OE=EB
∵直径AB垂直弦CD,
∴CE=ED
∴四边形OCBD是平行四边形,
∵AB垂直于弦CD,
∴四边形OCBD是菱形.
点评:本题考查了切线的判定,垂径定理等知识点.其中要证某直线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
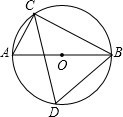 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=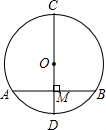 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )