题目内容
（2012•朝阳区二模）如图，在⊙O中，直径AB⊥弦CD于点H，E是⊙O上的点，若∠BEC=25°，则∠BAD的度数为（ ）分析：连接AC，根据直径AB⊥弦CD于点H，利用垂径定理得到
=
，从而利用等弧所对的圆周角相等得到∠CAB=∠DAB，利用圆周角定理得到∠BAD=∠BAC=25°．
 |
| BC |
|
| BD |
解答：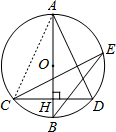
解：连接AC，
∵直径AB⊥弦CD于点H，
∴
=
∴∠CAB=∠DAB
∵∠BAC=∠BEC=25°，
∴∠BAD=∠BAC=25°．
故选C．
解：连接AC，∵直径AB⊥弦CD于点H，
∴
|
| BC |
|
| BD |
∴∠CAB=∠DAB
∵∠BAC=∠BEC=25°，
∴∠BAD=∠BAC=25°．
故选C．
点评：本题考查了圆周角定理及垂径定理的知识，解题的关键是构造辅助线得到等弧所对的圆周角相等．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
（2012•朝阳区二模）如图，直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α等于（ ）