题目内容
 如图,在直角坐标系中,点C(
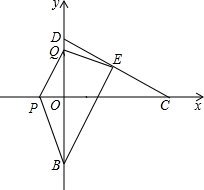
如图,在直角坐标系中,点C( ,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒
,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒 个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒.
个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒.
(1)求出点B的坐标;
(2)当t为何值时,△POQ与△COD相似?
(3)当点P在x轴负半轴上时,记四边形PBEQ的面积为S,求S关于t的函数关系式,并写出自变量的取值范围;
(4)在点P、Q的运动过程中,将△POQ绕点O旋转180°,点P的对应点P′,点Q的对应点Q′,当线段P′Q′与线段BE有公共点时,抛物线y=ax2+1经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M.由已知,直接写出:①a的取值范围为______;②点M移动的平均速度是______.
 解:(1)由题意得:OD=1,OC=
解:(1)由题意得:OD=1,OC= ,由勾股定理得:DC=2.
,由勾股定理得:DC=2.∵BE是DC的中垂线,
∴DE=1,∠DEB=90°.
在△DEB与△DOC中,
 ,
,∴△DEB≌△DOC(ASA),
∴BD=DC=2,
∴BO=1,
∴B(0,-1);
(2)分两种情况:
①当点P在x轴的正半轴上时,
由已知得,CP=
 ,OP=CO-CP=
,OP=CO-CP= ,OQ=t.
,OQ=t.由题意得:
 ,
,即:
 ,
, 解得
解得 ;
;②当点P在x轴的负半轴上时,
由题意得:
 ,
,即:
 ,
,解得
 .
.综上所述:当
 ,△POQ与△COD相似;
,△POQ与△COD相似;(3)S=S△PQB+S△EQB=
 =
=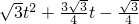 ,
,即S关于t的函数关系式为:S=
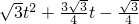 ,
,∵点P在x轴负半轴上,
∴t>
 ,
,又∵当点Q到达点D时,点P,Q同时停止运动,而点Q运动时间为1秒,
∴t≤1,
∴自变量t的取值范围为:
 <t≤1;
<t≤1; (4)①当P'Q'与BE有公共点时,初始位置点P′与点A重合,A为BE与x轴的交点.
(4)①当P'Q'与BE有公共点时,初始位置点P′与点A重合,A为BE与x轴的交点.由已知得,
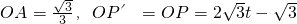 ,
,∴
 ,
,∴
 ,
,终止位置点P′与点C重合,点Q′与点B重合,这时t=1,
∴
 .
.设P'Q'的中点为F,当
 时,
时,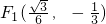 .
.把
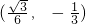 代入y=ax2+1,得:a=-16.
代入y=ax2+1,得:a=-16.当t=1时,
 ,
,把
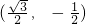 代入y=ax2+1,得:a=-2,
代入y=ax2+1,得:a=-2,∴a的取值范围为:-16≤a≤-2;
②初始位置的抛物线为y=-16x2+1,此时
 ,
,终止位置的抛物线为y=-2x2+1,此时
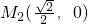 ,
,∴
 ,
,∵移动的时间为
 秒,
秒,∴点M移动的平均速度为每秒
 个单位.
个单位.故答案为-16≤a≤-2;每秒
 个单位.
个单位.分析:(1)先在直角△ODC中,由勾股定理求出DC=2,根据BE是DC的中垂线,得出DE=1,∠DEB=90°,再利用ASA证明△DEB≌△DOC,由全等三角形对应边相等得出BD=DC=2,则BO=1,进而求出B的坐标;
(2)由于点Q在线段OD上运动的时间为1秒,而点P用
 秒从C点运动到O点,则余下的
秒从C点运动到O点,则余下的 秒从O点运动到C关于y轴的对称点处,所以根据P点的不同位置分两种情况进行讨论:①当点P在x轴的正半轴上时,由于∠POQ=∠COD=90°,所以当△POQ与△COD相似时,又有两种情况,
秒从O点运动到C关于y轴的对称点处,所以根据P点的不同位置分两种情况进行讨论:①当点P在x轴的正半轴上时,由于∠POQ=∠COD=90°,所以当△POQ与△COD相似时,又有两种情况, ,用含t的代数式分别表示OP,OQ,列出关于t的比例式,解出即可;②当点P在x轴的负半轴上时,同①可求;
,用含t的代数式分别表示OP,OQ,列出关于t的比例式,解出即可;②当点P在x轴的负半轴上时,同①可求;(3)当点P在x轴负半轴上时,根据四边形PBEQ的面积为S=S△PQB+S△EQB,用含t的代数式代入即可求出S关于t的函数关系式,根据点P在x轴负半轴上及当点Q到达点D时,点P,Q同时停止运动即可求出自变量的取值范围;
(4)①当P'Q'与BE有公共点时,初始位置点P′与点A重合,则OP′=OP=OA,得出方程
 ,求出
,求出 ,终止位置点P′与点C重合,点Q′与点B重合,这时t=1,所以
,终止位置点P′与点C重合,点Q′与点B重合,这时t=1,所以 .
.再设P'Q'的中点为F,求出
 时,
时,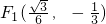 ,把
,把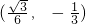 代入y=ax2+1,求得a=-16.当t=1时,同理求得a=-2,从而得出a的取值范围为:-16≤a≤-2;
代入y=ax2+1,求得a=-16.当t=1时,同理求得a=-2,从而得出a的取值范围为:-16≤a≤-2;②根据初始位置的抛物线为y=-16x2+1,求出
 ,根据终止位置的抛物线为y=-2x2+1,求出
,根据终止位置的抛物线为y=-2x2+1,求出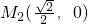 ,则
,则 ,又移动的时间为
,又移动的时间为 秒,根据速度=路程÷时间即可求出点M移动的平均速度为每秒
秒,根据速度=路程÷时间即可求出点M移动的平均速度为每秒 个单位.
个单位.点评:本题是二次函数的综合题型,其中涉及到勾股定理,全等三角形、相似三角形的判定与性质,四边形的面积,二次函数图象上点的坐标特征等知识,综合性较强,有一定难度.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: