题目内容
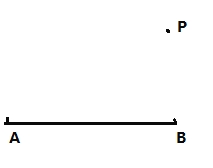
【题目】(1)如图,AB=4, ![]() O是以AB为直径的圆,以B为圆心,1为半径画弧与
O是以AB为直径的圆,以B为圆心,1为半径画弧与![]() O交于点C,连接AC.请按下列要求回答问题:
O交于点C,连接AC.请按下列要求回答问题:
①sin![]() A等于____________;
A等于____________;
②在线段AB上取一点E,当BE=______________时,连接CE,使线段CE与图中弦(不含直径)所夹角的正弦值等于![]() ;
;
(2)完成操作:仅用无刻度的直尺和圆规作一个直角三角形ABC,使![]() A的正弦值
A的正弦值
等于![]() .(保留作图痕迹,不必说明作法和理由)
.(保留作图痕迹,不必说明作法和理由)

【答案】(1)①![]() ;②
;②![]() 或2;(2)见解析.
或2;(2)见解析.
【解析】分析: (1)①根据直径所对的圆周角是直角得∠ACB=90°,再依据正弦的定义即可求出;
②题中不含直径的弦有BC和AC, 要满足线段CE与BC或AC所夹角的正弦值等于![]() ,即∠BCE=∠A或∠ACE=∠A,分情况即可求出;
,即∠BCE=∠A或∠ACE=∠A,分情况即可求出;
(2)作等边三角形△PMN,以MN为直径作⊙O,过点N作NF⊥MN,作∠PMN的平分线交NF于H,作∠MHN的平分线HB交MN于B,则BM=HM=2BN,以N为圆心NB为半径作弧交⊙O于P,连接MP、PN,△PMN即为所求.
详解: (1)∵AB为直径,
∴∠ACB=90°
又∵AB=4,BC=1
∴sinA=![]() .
.
故答案为: ![]() .
.
(2)∵sinA=![]() ,线段CE与图中弦所夹角的正弦值等于
,线段CE与图中弦所夹角的正弦值等于![]()
∴∠BCE=∠A或∠ACE=∠A,
当∠BCE=∠A时, CE⊥AB,
∴sin∠BCE=![]() =
=![]()
∴BE=![]() ,
,
当∠ACE=∠A时,CE=AE,则点O与点E重合,
∴BE=2.
综上,BE=![]() 或2.
或2.
(2)ABC即为所求.
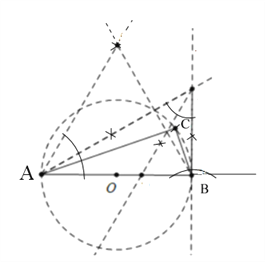
点睛: 本题考查作图-应用与设计,圆的有关知识,等边三角形的性质,锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型

练习册系列答案
相关题目