题目内容
【题目】如图,边![]() ,
,![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的两个动点,且始终保持
上的两个动点,且始终保持![]() ,若
,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为______.
的长为______.
【答案】![]() 或
或![]() 或3.
或3.
【解析】
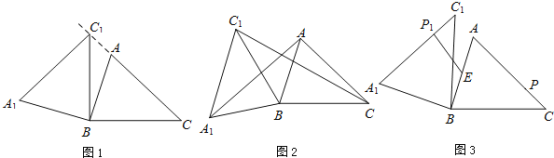
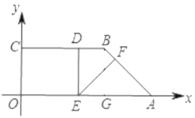
因为△AEF为等腰三角形,所以要分三种情况进行讨论:①当EF=AF时,如图1,根据△AGB是直角三角形及斜边AB=3可求AG的长,即BG的长,从而求出AE的长,相减即可得出OE;
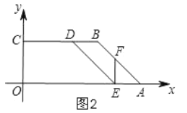
②当EF=AE时,如图2,AE=BD=![]() ,则OE=OA-AE即可;
,则OE=OA-AE即可;
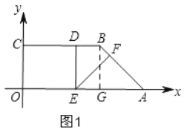
③当AE=AF时,如图3,证明△ODE是等腰三角形,再求OD的长,就是OE的长.
当![]() 为等腰三角形,存在3种情况:
为等腰三角形,存在3种情况:
①当![]() 时,如图1,过点
时,如图1,过点![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() 是直角三角形,
是直角三角形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∵![]() ,
,
∴![]() ,
,
则四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() ;
;
②当![]() ,如图2,
,如图2,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ;
;
③当![]() 时,如图3,
时,如图3,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
由(1)得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() 或3.
或3.


练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】为了迎接“六一”儿童节.某儿童运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋 价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?