题目内容
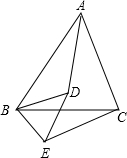已知，如图，D为△ABC内一点连接BD、AD，以BC为边在△ABC外作∠CBE=∠ABD，∠BCE=∠BAD，BE、CE交于E，连接DE．
（1）求证：
| BC |
| AB |
| BE |
| BD |
（2）求证：△DBE∽△ABC．
分析：（1）根据题意可知∠CBE=∠ABD，∠BCE=∠BAD可得出△CBE∽△ABD，再根据相似三角形的对应边成比例即可得出结论；
（2）由（1）知
=
，再由∠CBE=∠ABD可知∠DBE=∠ABC，故可得出△DBE∽△ABC．
（2）由（1）知
| BC |
| AB |
| BE |
| BD |
解答：证明：（1）在△CBE和△ABD中，
∵∠CBE=∠ABD，∠BCE=∠BAD，（1分）
∴△CBE∽△ABD．（2分）
∴
=
．（3分）
∴
=
．（4分）
即
=
；
（2）由（1）可知
=
，
∵∠CBE=∠ABD，
∴∠CBE+∠DBC=∠ABD+∠DBC．（5分）
即∠DBE=∠ABC．（6分）
∴△DBE∽△ABC．（7分）
∵∠CBE=∠ABD，∠BCE=∠BAD，（1分）
∴△CBE∽△ABD．（2分）
∴
| BC |
| AB |
| BE |
| BD |
∴
| BC |
| BE |
| AB |
| BD |
即
| BC |
| AB |
| BE |
| BD |
（2）由（1）可知
| BC |
| AB |
| BE |
| BD |
∵∠CBE=∠ABD，
∴∠CBE+∠DBC=∠ABD+∠DBC．（5分）
即∠DBE=∠ABC．（6分）
∴△DBE∽△ABC．（7分）
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的判定定理是解答此题的关键．
练习册系列答案
相关题目
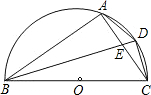
点E．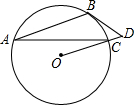
已知：如图，AB为⊙O的弦，过点O作AB的平行线，交⊙O于点C，直线OC上一点D满足∠D=∠ACB．
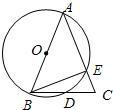已知：如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45度．给出以下五个结论：①∠EBC=22.5°；②BD=DC；③AE=2EC；④劣弧AE是劣弧DE的2倍；⑤AE=BC．其中正确结论的序号是（ ）
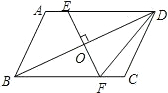已知：如图，BD为ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．求证：DE=DF．
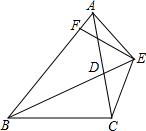已知：如图，BD为∠ABC的角平分线，且BD=BC，E为BD的延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①∠ABE=∠ACE；②∠BCE+∠BCD=180°；③AE=EC；④BE+BD=2BF，其中正确的是（ ）