题目内容
【题目】如图,设椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是 ![]() .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
【答案】
(1)解:∵椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,∴a=2,
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,∴a=2,
又∵椭圆C1的离心率是 ![]() .∴c=
.∴c= ![]() ,b=1,∴椭圆C1的标准方程:
,b=1,∴椭圆C1的标准方程: ![]()
(2)解:过点F(2,0)的直线l的方程设为:x=my+2,设A(x1,y1),B(x2,y2)
联立 ![]() 得y2﹣8my﹣16=0.
得y2﹣8my﹣16=0.
y1+y2=8m,y1y2=﹣16,∴|AB|= ![]() =8(1+m2).
=8(1+m2).
过F且与直线l垂直的直线设为:y=﹣m(x﹣2)
联立 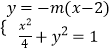 得(1+4m2)x2﹣16m2x+16m2﹣4=0,
得(1+4m2)x2﹣16m2x+16m2﹣4=0,
xC+2= ![]() ,xC=
,xC= ![]() .
.
∴|CF|= ![]()
![]() .
.
△ABC面积s= ![]() |AB||CF|=
|AB||CF|= ![]() .
.
令 ![]() ,则s=f(t)=
,则s=f(t)= ![]() ,f′(t)=
,f′(t)= ![]() ,
,
令f′(t)=0,则t2= ![]() ,即1+m2=
,即1+m2= ![]() 时,△ABC面积最小.
时,△ABC面积最小.
即当m=± ![]() 时,△ABC面积的最小值为9,此时直线l的方程为:x=±
时,△ABC面积的最小值为9,此时直线l的方程为:x=± ![]() y+2
y+2
【解析】(1)由已知可得a,又由椭圆C1的离心率得c,b=1即可.(2)过点F(2,0)的直线l的方程设为:x=my+2,设A(x1 , y1),B(x2 , y2)联立 ![]() 得y2﹣8my﹣16=0.|AB|=
得y2﹣8my﹣16=0.|AB|= ![]() ,同理得|CF|=
,同理得|CF|= ![]()
![]() .△ABC面积s=
.△ABC面积s= ![]() |AB||CF|=
|AB||CF|= ![]() .令
.令 ![]() ,则s=f(t)=
,则s=f(t)= ![]() ,利用导数求最值即可.
,利用导数求最值即可.

【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D , 过D作DE∥BC , 且DE=CD , 连接CE , 
(1)求证:△CDE为等边三角形;
(2)请连接BE , 若AB=4,求BE的长.
【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
项目 | 教学能力 | 科研能力 | 组织能力 |
甲 | 86 | 93 | 73 |
乙 | 81 | 95 | 79 |

(1)根据实际需要,将阅读能力、科研能力、组织能力三项测试得分按5:3:2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.


