题目内容
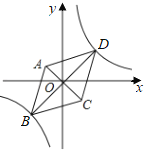
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点B、D在反比例函数y═
（k＞0）的图象上，对角线AC与BD相交于坐标原点O，若点A（﹣1，2），菱形的边长为5，则k的值是（ ）
A.4B.8C.12D.16
【答案】B
【解析】
根据菱形的性质得到AC⊥BD，根据勾股定理得到OA＝
，OD＝
＝
，求得直线AC的解析式为y＝﹣2x，求得BD的解析式为y＝2x，设D（a，2a），根据勾股定理即可得到结论．
解：∵四边形ABCD是菱形，
∴AC⊥BD，
∵点A（﹣1，2），
∴OA＝，
∵菱形的边长为5，
∴AD＝5，
∴OD＝ ＝，
∵对角线AC与BD相交于坐标原点O，
∴直线AC的解析式为y＝﹣2x，
∴BD的解析式为y＝2x，
设D（a，2a），
∴
，
∴a＝2（负值舍去），
∴D（2，4），
∵D在反比例函数y=
（k＞0）的图象上，
∴k＝2×4＝8，
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了选拔中考命题教师，某省的领导对全省数学教师进行抽样调查，要求每位数学教师从命制“抛物线综合题”“圆的难题”“解决实际问题”“简单题”“客观题”中自主选择一个类型，并将结果绘制成如下的统计图表：（100%回卷率，均为有效问卷）
题型 | 抛物线 综合题 | 圆的 难题 | 解决实 际问题 | 简单 题 | 客观 题 |
人数 | 2 | 3 | 4 | a | b |
请根据统计图表的信息回答下列问题
（1）填空：a=________；b=_________；并补全扇形统计图．
（2）若全省有2000名数学教师，试估计可以选中命制“解决实际问题”的老师有多少位？
（3）为选拔出今年数学中考解决实际问题的题目，现在领导要让擅长命制解决实际问题的4位老师：甲、乙、丙、丁分别命题，从其中选中2道题作为中考A卷和B卷上的题目．用列表法或者列树状图的办法求甲老师和丙老师命制的题目同时被选中的概率．
