题目内容
【题目】[问题提出]
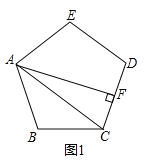
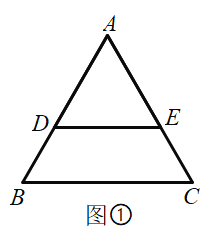
（1）如图
均为等边三角形，点
分别在边
上．将
绕点
沿顺时针方向旋转，连结
．在图
中证明
．
[学以致用]
（2）在
的条件下，当点
在同一条直线上时，
的大小为 度．
[拓展延伸]
（3）在的条件下，连结
．若
直接写出
的面积
的取值范围．
【答案】（1）见解析；（2）60或120；（3）
【解析】
（1）运用SAS证明
即可；
（2）分“当点
在线段
上”和“当点在线段的延长线上”两种情况求出
的大小即可；
（3）分别求出
的面积最大值和最小值即可得到结论
（1）
均为等边三角形，
，
，
，
即
在
和
中
；
（2）当
在同一条直线上时，分两种情况：
①当点在线段上时，如图，
∵
是等边三角形，
，
，
由（1）可知，
，
，
②当点在线段的延长线上时，如图，
是等边三角形，
，
由（1）可知，
，
综上所述，的大小为
或
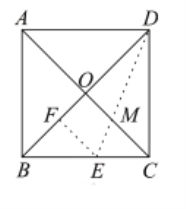
（3）过点A作
于点F，当点D在线段AF上时，点D到BC的距离最短，此时，点D到BC的距离为线段DF的长，如图：
是等边三角形，，
，
此时
；
当D在线段FA的延长线上时，点D到BC的距离最大，此时点D到BC的距离为线段DF的长，如图，
是等边三角形，，
，，
此时，
；
综上所述，的面积S 取值是
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
【题目】下面是十堰市的三个旅游景点：丹江口的武当山、房县的野人洞、郧西县的五龙河的部分门票价格表．某单位在国庆长假前期给每人购买了一张门票，现将购买门票的情况绘制成如图所示的柱状统计图．
景点 | 标价（元/张） |
武当山 | 200 |
野人洞 |
|
五龙河 | 80 |
请依据上表、图回答下列问题：
（1）去武当山旅游的门票有________张，购买去野人洞旅游的门票占所有门票张数的____________
．
（2）若该单位采取随机抽取的方式把门票分配给员工，在看不到门票的前提下，每人抽取一张（所有门票形状、大小、颜色等完全相同且充分洗匀）．问员工小红抽取去武当山的门票的概率是___________．
（3）若购买去五龙河的总款数占全部款数的
．试求出每张野人洞门票的价格．
