ÌâÄżÄÚÈĘ
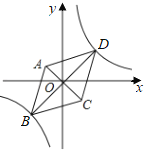
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÖ±Ïß![]() ·Ö±đÓëxÖ᥹yÖáÏàœ»ÓÚ”ăBĄąCŁŹŸčę”ăBĄąC”ÄĆŚÎïÏß
·Ö±đÓëxÖ᥹yÖáÏàœ»ÓÚ”ăBĄąCŁŹŸčę”ăBĄąC”ÄĆŚÎïÏß![]() ÓëxÖá”ÄÁíÒ»žöœ»”ăÎȘAŁš-1ŁŹ0Ł©Łź
ÓëxÖá”ÄÁíÒ»žöœ»”ăÎȘAŁš-1ŁŹ0Ł©Łź
Łš1Ł©ÇóŐâžöĆŚÎïÏߔıíŽïÊœŁ»
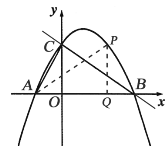
Łš2Ł©ÒŃÖȘ”ăDÔÚĆŚÎïÏßÉÏŁŹÇÒșáŚű±êÎȘ2ŁŹÇółöĄśBCD”ÄĂæ»ęŁ»
Łš3Ł©”ăPÊÇÖ±ÏßBCÉÏ·œ”ÄĆŚÎïÏßÉÏÒ»¶Ż”㣏čę”ăPŚśPQŽčÖ±ÓÚxÖᣏŽčŚăÎȘQŁźÊÇ·ńŽæÔÚ”ăPŁŹÊč”ĂÒÔ”ăAĄąPĄąQÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜BOCÏàËÆŁżÈôŽæÔÚŁŹÇëÇółö”ăP”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź


ĄŸŽđ°žĄżŁš1Ł©![]() Ł»Łš2Ł©
Ł»Łš2Ł©![]() Ł»Łš3Ł©”ăP”ÄŚű±êÎȘŁș
Ł»Łš3Ł©”ăP”ÄŚű±êÎȘŁș![]() »ò
»ò![]() Łź
Łź
ĄŸœâÎöĄż
Łš1Ł©±ŸÌâĐèÏÈžùŸĘÖ±ÏßčęBŁŹCÁœ”㣏Çó”ĂBŁŹC”ÄŚű±êŁŹÈ»șóžùŸĘ”Ķ«ÎśÊÇŒŽżÉ”ĂłöĆŚÎïÏߔĜâÎöÊœŁź
Łš2Ł©°ŃD”ÄșáŚű±êŽúÈëĆŚÎïÏߔĜâÎöÊœÇó”ĂŚĘŚű±êŁŹÇó”ĂËıßĐÎOBDCÊÇÌĘĐÎŁŹżÉÖ±œÓžùŸĘÈęœÇĐÎĂæ»ęč«ÊœÇó”ĂŁ»
Łš3Ł©±ŸÌâÊŚÏÈĆĐ¶ÏłöŽæÔÚŁŹÊŚÏÈÉè”ăP”ÄșáŚű±êÎȘmŁŹÔòP”ÄŚĘŚű±êÎȘ![]() ŁŹÔÙ·ÖÁœÖÖÇéżöœűĐĐÌÖÂÛŁș”±
ŁŹÔÙ·ÖÁœÖÖÇéżöœűĐĐÌÖÂÛŁș”±![]() ʱșÍ”±
ʱșÍ”±![]() ʱŁŹ”ĂłöĄśAPQĄŚĄśBCOŁŹĄśAPQĄŚĄśCBOŁŹ·Ö±đÇółö”ăP”ÄŚű±êŒŽżÉŁź
ʱŁŹ”ĂłöĄśAPQĄŚĄśBCOŁŹĄśAPQĄŚĄśCBOŁŹ·Ö±đÇółö”ăP”ÄŚű±êŒŽżÉŁź
Łš1Ł©ĄßÖ±Ïß![]() ·Ö±đÓëxÖ᥹yÖáÏàœ»ÓÚ”ăBĄąCŁŹ
·Ö±đÓëxÖ᥹yÖáÏàœ»ÓÚ”ăBĄąCŁŹ
ĄàBŁš3ŁŹ0Ł©ŁŹCŁš0ŁŹ2Ł©ŁŹ
œ«AŁš-1ŁŹ0Ł©ŁŹCŁš0ŁŹ2Ł©ŽúÈë![]() ”ĂŁŹ
”ĂŁŹ
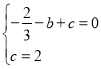 ŁŹ
ŁŹ
œâ”Ă![]() Łź
Łź
čÊŽËĆŚÎïÏߔĜâÎöÊœÎȘ![]() Łź
Łź
Łš2Ł©ÈçÍŒŁŹčę”ă![]() Śś
Śś![]()
![]()
![]() Öᣏœ»Ö±Ïß
Öᣏœ»Ö±Ïß![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹ
ŁŹ
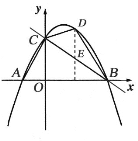
ÓÉ![]() Áî
Áî![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
Ąà![]()
ÓÉ![]() ŁŹÁî
ŁŹÁî![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁŹ
ŁŹ
Ąà![]()
Ąà![]()
![]() Łź
Łź
Ąà![]()
Łš3Ł©Éè”ă![]() ”ÄșáŚű±êÎȘ
”ÄșáŚű±êÎȘ![]() ŁŹÔò
ŁŹÔò![]()
![]() Ł©ŁŹ
Ł©ŁŹ![]()
ąÙ”±![]() ĄŚ
ĄŚ![]() ʱŁŹ
ʱŁŹ![]() ŁŹŒŽ
ŁŹŒŽ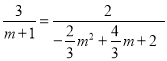 ŁŹ
ŁŹ
œâ”ĂŁŹ![]() ŁŹ
ŁŹ![]() ŁšÉáÈ„Ł©ŁŹŽËʱ
ŁšÉáÈ„Ł©ŁŹŽËʱ![]() Łź
Łź
ąÚ”±![]() ĄŚ
ĄŚ![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
ŒŽ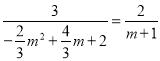 ŁŹ
ŁŹ
œâ”ĂŁŹ![]() ŁŹ
ŁŹ![]() ŁšÉáÈ„Ł©ŁŹŽËʱ
ŁšÉáÈ„Ł©ŁŹŽËʱ![]() Łź
Łź
ËùÒÔ”ăP”ÄŚű±êÎȘŁș![]() »ò
»ò![]()

 ÊîŒÙŚśÒ”ÊîŒÙżìÀÖÁ·Îś°Čłö°æÉçÏ”ÁĐŽđ°ž
ÊîŒÙŚśÒ”ÊîŒÙżìÀÖÁ·Îś°Čłö°æÉçÏ”ÁЎ𰞥ŸÌâÄżĄżÊĐÉÙÄêčŹÎȘХѧÉúżȘÉèÁË»æ»ĄąÒôÀÖĄąÎ蔞șÍőÌÈ”ÀËÄÀàĐËÈ€°àŁŹÎȘÁËœâѧÉú¶ÔŐâËÄÀàĐËÈ€°à”ÄÏČ°źÇéżöŁŹ¶ÔѧÉúœűĐĐÁËËæ»úÎÊŸí”śČé(ÎÊŸí”śČé±íÈçÍŒËùÊŸ)ŁŹœ«”śČéœáčûŐûÀíșó»æÖÆÁËÒ»·ùČ»ÍêŐû”ÄÍłŒÆ±í

ĐËÈ€°à | Æ”Êę | Æ”ÂÊ |
|
|
|
|
|
|
|
|
|
|
| |
șÏŒÆ |
|
ÇëÄăžùŸĘÍłŒÆ±íÖĐÌáč©”ÄĐĆÏą»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©ÍłŒÆ±íÖĐ”Ä![]() _____ŁŹ
_____ŁŹ![]() Ł»
Ł»
Łš2Ł©žùŸĘ”śČéœáčûŁŹÇëÄăčÀŒÆžĂÊĐ![]() ĂûХѧÉúÖĐŚîÏČ»¶Ą°»æ»Ą±ĐËÈ€°à”ÄÈËÊꣻ
ĂûХѧÉúÖĐŚîÏČ»¶Ą°»æ»Ą±ĐËÈ€°à”ÄÈËÊꣻ
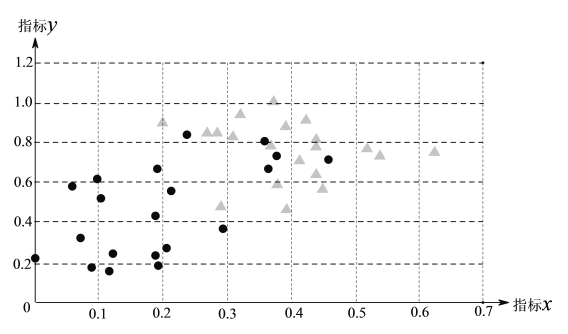
Łš3Ł©ÍőÇżșÍÀîê»ŃĄÔńČÎŒÓĐËÈ€°àŁŹÈôÍőÇżŽÓ![]() ÈęÀàĐËÈ€°àÖĐËæ»úŃĄÈĄÒ»ÀàŁŹÀîÎâŽÓ
ÈęÀàĐËÈ€°àÖĐËæ»úŃĄÈĄÒ»ÀàŁŹÀîÎâŽÓ![]() ÈęÀàĐËÈ€°àÖĐËæ»úŃĄÈĄÒ»ÀàŁŹÇëÓĂ»ÊśŚŽÍŒ»òÁбížń”Ä·œ·šŁŹÇóÁœÈËÇĄșĂŃĄÖĐÍŹÒ»ÀàĐËÈ€°à”ÄžĆÂÊŁź
ÈęÀàĐËÈ€°àÖĐËæ»úŃĄÈĄÒ»ÀàŁŹÇëÓĂ»ÊśŚŽÍŒ»òÁбížń”Ä·œ·šŁŹÇóÁœÈËÇĄșĂŃĄÖĐÍŹÒ»ÀàĐËÈ€°à”ÄžĆÂÊŁź
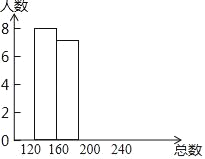
ĄŸÌâÄżĄżÎȘĆàŃűѧÉúÍ„șĂ”ÄŃ§Ï°Ï°čߣŹÄłĐŁŸĆÄꌶÄꌶŚéŸÙĐĐĄ°ŐûÀíŽíÌâŒŻĄ°”ÄŐśŒŻŐčÊŸ»î¶ŻŁŹČąËæ»ú¶ÔČż·ÖѧÉúÈęÄêĄ°ŐûÀíÌâŒŻĄ±ÖĐÊŐŒŻ”ÄŽíÌâÊęxœűĐĐÁËłéŃù”śČ飏žùŸĘÊŐŒŻ”ÄÊęŸĘ»æÖÆÁËÏÂĂæČ»ÍêŐû”ÄÍłŒÆÍŒ±íŁź
·ÖŚé | Æ”Êę | Æ”ÂÊ |
”ÚÒ»ŚéŁš0ĄÜxŁŒ120Ł© | 3 | 0.15 |
”Ú¶țŚéŁš120ĄÜxŁŒ160Ł© | 8 | a |
”ÚÈęŚéŁš160ĄÜxŁŒ200Ł© | 7 | 0.35 |
”ÚËČ飚200ĄÜxŁŒ240Ł© | b | 0.1 |
ÇëÄăžùŸĘÍŒ±íÖĐ”ÄĐĆÏąÍêłÉÏÂÁĐÎÊÌâŁș
Łš1Ł©Æ”Êę·ÖČŒ±íÖĐaŁœĄĄ ĄĄŁŹbŁœĄĄ ĄĄŁŹČąœ«ÍłŒÆÍŒČčłäÍêŐûŁ»
Łš2Ł©ÈçčûžĂĐŁŸĆÄꌶčČÓĐѧÉú360ÈËŁŹčÀŒÆŐûÀí”ÄŽíÌâÊęÔÚ160»ò160ÌâÒÔÉÏ”ÄѧÉúÓжàÉÙÈËŁż
Łš3Ł©ÒŃÖȘ”ÚÒ»ŚéÖĐÓĐÁœžöÊÇŒŚ°àѧÉúŁŹ”ÚËÄŚéÖĐÓĐÒ»žöÊÇŒŚ°àѧÉúŁŹÀÏÊŠËæ»úŽÓŐâÁœžöŚéÖĐžśŃĄÒ»ĂûѧÉúÌžŐûÀíŽíÌâ”ÄÌć»áŁŹÔòËùŃĄÁœÈËŐęșöŒÊÇŒŚ°àѧÉú”ÄžĆÂÊÊǶàÉÙŁż