题目内容
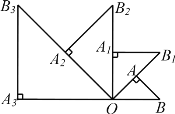
【题目】如图,△ OAB 是腰长为 1 的等腰直角三角形, OAB 90°,延长OA 至 B1 ,使 AB1 OA ,以OB1 为底,在△ OAB 外侧作等腰直角三角形OA1B1 ,再延长OA1 至 B2 , 使 A1B2 OA1 ,以OB2 为底,在△ OA1B1 外侧作等腰直角三角形OA2 B2 ,……,按此规律作等腰直角三角形OAn Bn ( n 1 , n 为正整数),回答下列问题:
(1) A3B3 的长是_____________;(2)△ OA2020 B2020 的面积是_____________.
【答案】![]()
![]()
【解析】
(1)根据等腰直角三角形的性质得到AB=OA=1,A1B1=![]() AB,A2B2=
AB,A2B2=![]() A1B1=2AB,A3B3=
A1B1=2AB,A3B3=![]() A2B2=
A2B2=![]() AB,故可求解;
AB,故可求解;
(2)先依次求出△OAB,△OA1B1,△OA2B2,△OA3B3的面积,找到变化规律即可求解△ OA2020 B2020 的面积.
(1)∵△ OAB 是腰长为 1 的等腰直角三角形, OAB 90°,延长OA 至 B1 ,使 AB1 OA ,以OB1 为底,在△ OAB 外侧作等腰直角三角形OA1B1 ,
∴OB1=2OA=2,设A1O=x,则A1O= A1B1=x
根据A1O2+A1B12= OB12,x2+x2= 22,
得x=![]() ,
,
故A1B1=![]()
同理可得A2B2=![]() A1B1=2AB,A3B3=
A1B1=2AB,A3B3=![]() A2B2=
A2B2=![]() AB=
AB=![]() ,
,
∴A3B3=![]() ;
;
(2)∵△ OAB 是腰长为 1 的等腰直角三角形
∴△OAB的面积为![]() =
=![]() ;
;
∵A1B1=![]() AB=
AB=![]()
∴△OA1B1的面积为![]() =
=![]() ;
;
∵A2B2=![]() A1B1=2
A1B1=2
∴△OA2B2的面积为![]() ;
;
∵A3B3=2![]()
∴△OA3B3的面积为![]() ;
;
…
∴△OAnBn的面积为![]() ;
;
故△ OA2020 B2020 的面积是![]()
故填:(1). ![]() (2).
(2). ![]()