Question

【题目】如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（ ）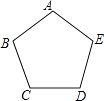

A.（2，﹣3）
B.（2，3）
C.（3，2）
D.（3，﹣2）

Answer 1

【答案】C
【解析】解：∵点A坐标为（0，a），

∴点A在该平面直角坐标系的y轴上，

∵点C、D的坐标为（b，m），（c，m），

∴点C、D关于y轴对称，

∵正五边形ABCDE是轴对称图形，

∴该平面直角坐标系经过点A的y轴是正五边形ABCDE的一条对称轴，

∴点B、E也关于y轴对称，

∵点B的坐标为（﹣3，2），

∴点E的坐标为（3，2）．

故答案为：C．

由题意得出y轴的位置，由正五边形ABCDE是轴对称图形，根据关于y轴对称点的坐标特点，即可求出点E的坐标。