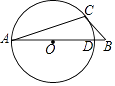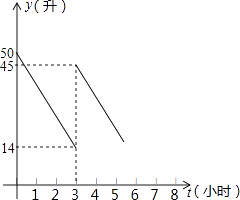ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy=©x+3ÓėÅ×ĪļĻß ![]() ½»ÓŚA”¢BĮ½µć£¬µćAŌŚxÖįÉĻ£¬µćBµÄŗį×ų±źĪŖ
½»ÓŚA”¢BĮ½µć£¬µćAŌŚxÖįÉĻ£¬µćBµÄŗį×ų±źĪŖ ![]() £®¶ÆµćPŌŚÅ×ĪļĻßÉĻŌĖ¶Æ£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻߣ¬½»Ö±ĻßABÓŚµćQ£®µ±PQ²»ÓėyÖįÖŲŗĻŹ±£¬ŅŌPQĪŖ±ß×÷Õż·½ŠĪPQMN£¬Ź¹MNÓėyÖįŌŚPQµÄĶ¬²ą£¬Į¬½įPM£®ÉčµćPµÄŗį×ų±źĪŖm£®
£®¶ÆµćPŌŚÅ×ĪļĻßÉĻŌĖ¶Æ£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻߣ¬½»Ö±ĻßABÓŚµćQ£®µ±PQ²»ÓėyÖįÖŲŗĻŹ±£¬ŅŌPQĪŖ±ß×÷Õż·½ŠĪPQMN£¬Ź¹MNÓėyÖįŌŚPQµÄĶ¬²ą£¬Į¬½įPM£®ÉčµćPµÄŗį×ų±źĪŖm£®
£Ø1£©Ēób”¢cµÄÖµ£®
£Ø2£©µ±µćNĀäŌŚÖ±ĻßABÉĻŹ±£¬Ö±½ÓŠ“³ömµÄȔֵ·¶Ī§£®
£Ø3£©µ±µćPŌŚA”¢BĮ½µćÖ®¼äµÄÅ×ĪļĻßÉĻŌĖ¶ÆŹ±£¬ÉčÕż·½ŠĪPQMNµÄÖܳ¤ĪŖC£¬ĒóCÓėmÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öCĖęmŌö“ó¶ųŌö“óŹ±mµÄȔֵ·¶Ī§£®
£Ø4£©µ±”÷PQMÓė×ų±źÖįÓŠ2øö¹«¹²µćŹ±£¬Ö±½ÓŠ“³ömµÄȔֵ·¶Ī§£®
”¾“š°ø”æ
£Ø1£©½ā£ŗ”ßÖ±Ļßy=©x+3ÓėxÖįĻą½»ÓŚµćA£¬
”ąA£Ø3£¬0£©£¬
”ßµćBŌŚÖ±Ļßy=©x+3ÉĻ£¬ĒŅBµÄŗį×ų±źĪŖ© ![]() £¬
£¬
”ąB£Ø© ![]() £¬
£¬ ![]() £©£¬
£©£¬
”ßA£¬BŌŚÅ×ĪļĻßÉĻ£¬
”ą  £¬
£¬
”ą ![]()
£Ø2£©½ā£ŗ·½·Ø1”¢ÓÉ£Ø1£©ÖŖ£¬b= ![]() £¬c=
£¬c= ![]() £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=© ![]() x2+
x2+ ![]() x+
x+ ![]() £¬
£¬
ÉčP£Øm£¬© ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¬
£©£¬
”ßµćQŌŚÖ±Ļßy=©x+3ÉĻ£¬
”ąQ£Øm£¬©m+3£©£¬
”ßµćNŌŚÖ±ĻßABÉĻ£¬
”ąN£Ø£Ø ![]() m2©
m2© ![]() m©
m© ![]() £©£¬£Ø©
£©£¬£Ø© ![]() m2+
m2+ ![]() m+
m+ ![]() £©£©£¬
£©£©£¬
”ąPN=| ![]() m2©
m2© ![]() m©
m© ![]() ©m|=|
©m|=| ![]() m2©
m2© ![]() m©
m© ![]() |
|
”ąPQ=|© ![]() m2+
m2+ ![]() m+
m+ ![]() ©£Ø©m+3£©|=|©
©£Ø©m+3£©|=|© ![]() m2+
m2+ ![]() m+
m+ ![]() |£¬
|£¬
”ßĖıߊĪPQMNŹ±Õż·½ŠĪ£¬
”ąPN=PQ£¬
”ą| ![]() m2©
m2© ![]() m©
m© ![]() |=|©
|=|© ![]() m2+
m2+ ![]() m+
m+ ![]() |£¬“ĖŹ±µČŹ½ŗć³ÉĮ¢£¬
|£¬“ĖŹ±µČŹ½ŗć³ÉĮ¢£¬
µ±m£¼0ĒŅm”Ł© ![]() Ź±£¬
Ź±£¬
”ßMNÓėyÖįŌŚPQµÄĶ¬²ą£¬
”ąµćNŌŚµćPÓŅ²ą£¬
”ą ![]() m2©
m2© ![]() m©
m© ![]() £¾m£¬
£¾m£¬
”ąm£¼© ![]() £¬
£¬
µ±m£¾0ĒŅm”Ł3Ź±£¬
”ßMNÓėyÖįŌŚPQµÄĶ¬²ą£¬
”ąµćPŌŚµćNµÄÓŅ²ą£¬
”ą ![]() m2©
m2© ![]() m©
m© ![]() £¼m£¬
£¼m£¬
”ą© ![]() £¼m£¼3£¬
£¼m£¼3£¬
”ą0£¼m£¼3£¬
¼“£ŗmµÄ·¶Ī§ĪŖm£¼© ![]() »ņ0£¼m£¼3£»
»ņ0£¼m£¼3£»
·½·Ø2”¢ČēĶ¼£¬

¼ĒÖ±ĻßABÓėyÖįµÄ½»µćĪŖD£¬
”ßÖ±ĻßABµÄ½āĪöŹ½ĪŖy=©x+3£¬
”ąD£Ø0£¬3£©£¬
”ąOD=3£¬
”ßA£Ø3£¬0£©£¬
”ąOA=3£¬
”ąOA=OB£¬
”ą”ĻODA=45”ć£¬
”ßPQ”ĪyÖį£¬
”ą”ĻPQB=45”ć£¬
¼Ē£ŗÖ±ĻßPN½»Ö±ĻßABÓŚN'£¬
”ßĖıߊĪPQMNŹĒÕż·½ŠĪ£¬
”ą”ĻQPN=90”ć£¬
”ą”ĻPN'Q=45”ć=”ĻPQN'£¬
”ąPQ=PN'£¬
”ßĖıߊĪPQMNŹĒÕż·½ŠĪ£¬
”ąPQ=PN£¬
µćNŌŚµćPµÄ×ó²ąŹ±£¬µćN'¶¼ŌŚÖ±ĻßABÉĻ£¬
”ßMNÓėyÖįŌŚPQµÄĶ¬²ą£¬
”ąmµÄ·¶Ī§ĪŖm£¼© ![]() »ņ0£¼m£¼3
»ņ0£¼m£¼3
£Ø3£©½ā£ŗÓÉ£Ø1£©ÖŖ£¬b= ![]() £¬c=
£¬c= ![]() £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=© ![]() x2+
x2+ ![]() x+
x+ ![]() £¬
£¬
ÉčP£Øm£¬© ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¬
£©£¬
”ßµćQŌŚÖ±Ļßy=©x+3ÉĻ£¬
”ąQ£Øm£¬©m+3£©£¬
”ąPQ=|© ![]() m2+
m2+ ![]() m+
m+ ![]() ©£Ø©m+3£©|=|©
©£Ø©m+3£©|=|© ![]() m2+
m2+ ![]() m+
m+ ![]() |£¬
|£¬
”ßµćPŌŚµćA£¬BÖ®¼äµÄÅ×ĪļĻßÉĻ£¬
”ąPQ=© ![]() m2+
m2+ ![]() m+
m+ ![]() £¬£Ø©
£¬£Ø© ![]() £¼m£¼3ĒŅm”Ł0£©£¬
£¼m£¼3ĒŅm”Ł0£©£¬
”ßÉčÕż·½ŠĪPQMNµÄÖܳ¤ĪŖC£¬
”ąC=4PQ=4£Ø© ![]() m2+
m2+ ![]() m+
m+ ![]() £©=©2m2+
£©=©2m2+ ![]() m+2=©2£Øm©
m+2=©2£Øm© ![]() £©2+
£©2+ ![]() £¬
£¬
”ßCĖęmŌö“ó¶ųŌö“ó£¬
”ąm£¼ ![]() £¬
£¬
”ą© ![]() £¼m£¼
£¼m£¼ ![]() ĒŅm”Ł0
ĒŅm”Ł0
£Ø4£©½ā£ŗµ±”÷PQMÓė×ų±źÖįÓŠ2øö¹«¹²µćŹ±£¬
”ąm£¼0»ņ0£¼m£¼3
µ±0£¼m£¼3£¬PN£¾yP£¬
ÓÉ£Ø2£©ÖŖ£¬P£Øm£¬© ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¬PQ=|©
£©£¬PQ=|© ![]() m2+
m2+ ![]() m+
m+ ![]() |=©
|=© ![]() m2+
m2+ ![]() m+
m+ ![]()
”ßĖıߊĪPQMNŹĒÕż·½ŠĪ£¬
”ąPN=PQ=© ![]() m2+
m2+ ![]() m+
m+ ![]() £¾©
£¾© ![]() m2+
m2+ ![]() m+
m+ ![]() £¬
£¬
”ąm£¾3£¬ĖłŅŌ£¬“ĖÖÖĒéæö²»·ūŗĻĢāŅā£»
µ±m£¼0Ź±£¬PN£¾yP£¬
”ßPQ= ![]() m2©
m2© ![]() m©
m© ![]() £¬
£¬
”ßĖıߊĪPQMNŹĒÕż·½ŠĪ£¬
”ąPN=PQ= ![]() m2©
m2© ![]() m©
m© ![]() £¾©
£¾© ![]() m2+
m2+ ![]() m+
m+ ![]() £¬
£¬
”ąm£¾3£ØÉį£©»ņm£¼© ![]() £¬
£¬
¼“£ŗµ±”÷PQMÓė×ų±źÖįÓŠ2øö¹«¹²µćŹ±£¬m£¼© ![]()
”¾½āĪö”æ£Ø1£©ĻČČ·¶Ø³öµćA£¬BµÄ×ų±ź£¬×īŗóÓĆ“ż¶ØĻµŹż·Ø¼“æÉµĆ³ö½įĀŪ”£
£Ø2£©µćPŌŚÅ×ĪļĻßÉĻ£¬µćQŌŚÖ±Ļßy=©x+3ÉĻ£¬µćNŌŚÖ±ĻßABÉĻ£¬Éč³öµćPµÄ×ų±ź£¬ŌŁ±ķŹ¾³öQ”¢NµÄ×ų±ź£¬¼“æÉµĆ³öPN=PQ£¬ŌŁÓĆMNÓėyÖįŌŚPQµÄĶ¬²ą£¬½ØĮ¢²»µČŹ½¼“æÉµĆ³ö½įĀŪ”£
£Ø3£©µćPŌŚµćA£¬BÖ®¼äµÄÅ×ĪļĻßÉĻ£¬øł¾Ż£Ø2£©æÉÖŖPQµÄ³¤£¬ÉčÕż·½ŠĪPQMNµÄÖܳ¤ĪŖC£¬øł¾ŻC=4PQ£¬½ØĮ¢CÓėmµÄŗÆŹż¹ŲĻµŹ½£¬Ēó³öĘ䶄µć×ų±ź£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬¼“æÉĒóµĆ½įĀŪ”£
£Ø4£©·ÖĮ½ÖÖĒéæöĢÖĀŪ¼ĘĖć¼“æÉĒó³ö½įĀŪ”£
”¾æ¼µć¾«Īö”æÕĘĪÕŅ»“ĪŗÆŹżµÄŠŌÖŹŗĶ¶ž“ĪŗÆŹżµÄ×īÖµŹĒ½ā“š±¾ĢāµÄøł±¾£¬ŠčŅŖÖŖµĄŅ»°ćµŲ£¬Ņ»“ĪŗÆŹży=kx+bÓŠĻĀĮŠŠŌÖŹ£ŗ£Ø1£©µ±k>0Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó£Ø2£©µ±k<0Ź±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£»Čē¹ū×Ō±äĮæµÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬ÄĒĆ“ŗÆŹżŌŚ¶„µć“¦Č”µĆ×ī“óÖµ£Ø»ņ×īŠ”Öµ£©£¬¼“µ±x=-b/2aŹ±£¬y×īÖµ=(4ac-b2)/4a£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æijŠ£¶ŌĘß”¢°Ė”¢¾ÅÄź¼¶µÄѧɜ½ųŠŠĢåÓżĖ®Ę½²āŹŌ£¬³É¼ØĘĄ¶ØĪŖÓÅŠć”¢Į¼ŗĆ”¢ŗĻøń”¢²»ŗĻøńĖÄøöµČµŚ£®ĪŖĮĖ½āÕā“Ī²āŹŌĒéæö£¬Ń§Š£“ÓČżøöÄź¼¶Ė껜³éČ”200ĆūѧɜµÄĢåÓż³É¼Ø½ųŠŠĶ³¼Ę·ÖĪö£®Ļą¹ŲŹż¾ŻµÄĶ³¼ĘĶ¼”¢±ķČēĻĀ£ŗ
ø÷Äź¼¶Ń§Éś³É¼ØĶ³¼Ę±ķ | ||||
ÓÅŠć | Į¼ŗĆ | ŗĻøń | ²»ŗĻøń | |
ĘßÄź¼¶ | a | 20 | 24 | 8 |
°ĖÄź¼¶ | 29 | 13 | 13 | 5 |
¾ÅÄź¼¶ | 24 | b | 14 | 7 |
øł¾ŻŅŌÉĻŠÅĻ¢½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŌŚĶ³¼Ę±ķÖŠ£¬aµÄÖµĪŖ £¬ bµÄÖµĪŖ£»
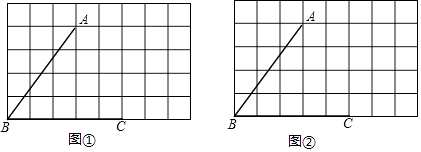
£Ø2£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬°ĖÄź¼¶Ėł¶ŌÓ¦µÄÉČŠĪŌ²ŠÄ½ĒĪŖ¶Č£»
£Ø3£©ČōøĆŠ£ČżøöÄź¼¶¹²ÓŠ2000Ćūѧɜ²Ī¼Óæ¼ŹŌ£¬ŹŌ¹Ą¼ĘøĆŠ£Ń§ÉśĢåÓż³É¼Ø²»ŗĻøńµÄČĖŹż£®
”¾ĢāÄæ”æij“åĪŖĮĖ¾”Ōē°ŚĶŃʶĒīĀäŗóµÄĻÖד£¬»ż¼«ĻģÓ¦¹ś¼ŅŗÅÕŁ£¬15Ī»“åĆń¼Æ׏8ĶņŌŖ£¬³Š°üĮĖŅ»Š©ĶĮµŲÖÖÖ²ÓŠ»śŹß²ĖŗĶĖ®¹ū£¬ÖÖÕāĮ½ÖÖ×÷ĪļĆ湫ĒźŠčŅŖČĖŹżŗĶĶ¶Čė׏½šČēĻĀ±ķ£ŗ
×÷ĪļÖÖĄą | Ć湫ĒźĖłŠčČĖŹż/ČĖ | Ć湫ĒźĶ¶Čė׏½š/ĶņŌŖ |
Źß²Ė | 4 | 2 |
Ė®¹ū | 5 | 3 |
ŌŚĻÖÓŠĢõ¼žĻĀ£¬Õā15Ī»“åĆńÓ¦³Š°ü¶ąÉŁ¹«ĒźĶĮµŲ£¬ŌõŃł°²ÅÅÄÜŹ¹ĆæČĖ¶¼ÓŠŹĀæÉ×ö£¬²¢ĒŅ׏½šÕżŗĆ¹»ÓĆ£æ