Question

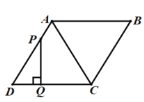
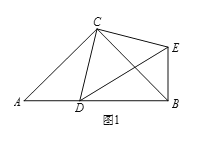
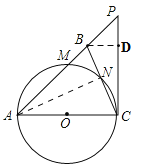
【题目】如图，在等腰三角形中，，以为直径的分别交、于点、，过点作的切线交的延长线于点．

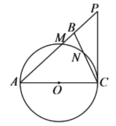
（1）求证：；

（2）若的半径为5，，求的周长．

Answer 1

【答案】（1）证明见解析；（2）40

【解析】

（1）证明AN平分∠BAC，则∠NAC+∠ACB=∠PCB+∠ACB=90°，∠NAC=∠BCP，即可证明；

（2）过点作，交于点，由三角函数，求出BC、BD的长度，得到CD的长度，再由平行线分线段成比例，得到，，即可得到答案．

（1）证明：连接，如图，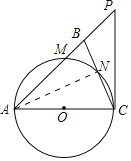

∵AC为直径，
∴AN⊥BC，
∵AB=AC，
∴AN平分∠BAC，
∵PC是圆的切线，
∴∠ACP=90°，
∵∠NAC+∠ACB=∠PCB+∠ACB=90°，
∴∠NAC=∠BCP，
即∠BAC=2∠BCP；

（2）解：过点作，交于点，

∵，

∴，

∴，

∴，

在中，

，

∴，

又∵

∴，

∴，，

∴的周长是．