题目内容
【题目】(1)问题发现
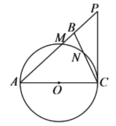
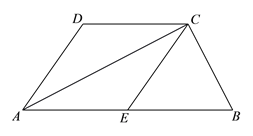
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
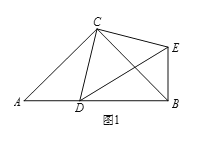
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
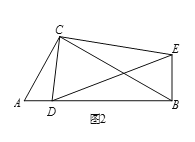
(3)拓展延伸
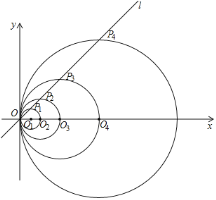
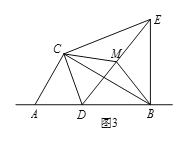
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
【答案】(1)1,90°;(2)![]() ,90°,理由见解析;(3)3+
,90°,理由见解析;(3)3+![]() 或3-
或3-![]()
【解析】
(1)易得△ABC和△CDE为等腰直角三角形,所以AC=BC,CD=CE,通过证明△ACD≌△BCE,可得AD=BE和∠CAD=∠CBE=45°,进而得出答案;
(2)通过证明△ACD∽△BCE,可得![]() 的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
(3)分点D在线段AB上和BA延长线上两种情况讨论,由直角三角形的性质可证CM=BM=![]() ,即可求DE=
,即可求DE=![]() ,由相似三角形的性质可得∠ABE=90°,BE=
,由相似三角形的性质可得∠ABE=90°,BE=![]() AD,由勾股定理可求BE的长.
AD,由勾股定理可求BE的长.
解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,
∴∠ABC=∠CAB=45°,∠CDE=∠CED=45°
∴AC=BC,CD=CE
∵∠ACD+∠BCD=∠BCE+∠BCD=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE=45°
∴![]() =1,∠DBE=∠ABC+∠CBE=90°
=1,∠DBE=∠ABC+∠CBE=90°
故答案为:1,90°;
(2)![]() =
=![]() ,∠DBE=90°,理由如下:
,∠DBE=90°,理由如下:
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴∠ACD=∠BCE,∠CED=∠ABC=30°,
∴tan∠ABC=tan30°=![]() =
=![]() .
.
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴Rt△ACB∽Rt△DCE,
∴![]() =
=![]() ,且∠ACD=∠BCE,
,且∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() =
=![]() =
=![]() ,∠CBE=∠CAD=60°,
,∠CBE=∠CAD=60°,
∴∠DBE=∠ABC+∠CBE=90°;
(3)若点D在线段AB上,如图,
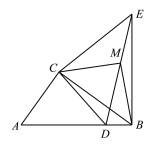
由(2)知:![]() =
=![]() =
=![]() ,∠ABE=90°,
,∠ABE=90°,
∴BE=![]() AD,
AD,
∵AC=2,∠ACB=90°,∠CAB=60°,
∴AB=4,BC=2![]() .
.
∵∠ECD=∠ABE=90°,且点M是DE中点,
∴CM=BM=![]() DE,
DE,
且△CBM是直角三角形,
∴CM2+BM2=BC2=(2![]() )2,
)2,
∴BM=CM=![]() ,
,
∴DE=2![]() ,
,
∵DB2+BE2=DE2,
∴(4-AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() +1,
+1,
∴BE=![]() AD=3+
AD=3+![]() ;
;
若点D在线段BA延长线上,如图,
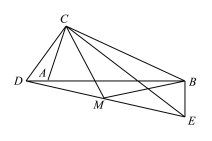
同理可得:DE=2![]() ,BE=
,BE=![]() AD,
AD,
∵BD2+BE2=DE2,
∴(4+AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() -1,
-1,
∴BE=![]() AD=3-
AD=3-![]() .
.
综上所述:BE的长为3+![]() 或3-
或3-![]() .
.

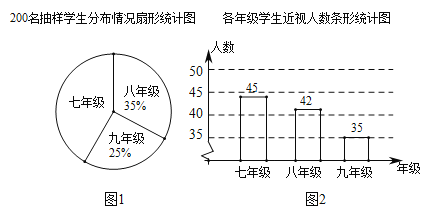
 口算能手系列答案
口算能手系列答案【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.