题目内容
24、阅读材料并解答问题：
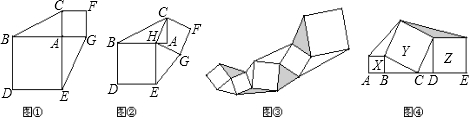
很多代数原理，可以用几何模型来表示．例如：代数恒等式（2a+b）（a+b）=2a2+3ab+b2，可以用图1或图2等图形的面积表示．
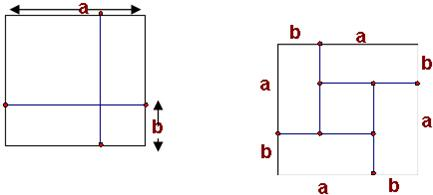
（1）请写出图3所表示的代数恒等式：
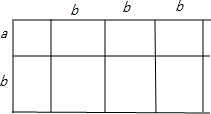
（2）试画出一个几何图形，使它的面积能表示：（a+b）（a+3b）=a2+4ab+3b2
（3）下列有几张如图所示的卡片，用它们拼一些新的图形，验证下列两个公式：
（1）（a-b）2=a2-2ab+b2 （2）（a+b）2-（a-b）2=4ab
很多代数原理，可以用几何模型来表示．例如：代数恒等式（2a+b）（a+b）=2a2+3ab+b2，可以用图1或图2等图形的面积表示．
（1）请写出图3所表示的代数恒等式：
（a+2b）（2a+b）=2a2+5ab+2b2
（2）试画出一个几何图形，使它的面积能表示：（a+b）（a+3b）=a2+4ab+3b2
（3）下列有几张如图所示的卡片，用它们拼一些新的图形，验证下列两个公式：
（1）（a-b）2=a2-2ab+b2 （2）（a+b）2-（a-b）2=4ab
分析：（1）根据图形的总面积等于各个部分的面积的和，即可写出；
（2）根据图形的总面积等于各个部分的面积的和，可以作一个一边是a+b，另一边是a+3b的矩形；
（3）同理即可作出图形．
（2）根据图形的总面积等于各个部分的面积的和，可以作一个一边是a+b，另一边是a+3b的矩形；
（3）同理即可作出图形．
解答：解：（1）答案是：（a+2b）（2a+b）=2a2+5ab+2b2
（2）
（3）每个图（3分）
（2）
（3）每个图（3分）
点评：本题主要考查了乘法公式的几何表示，正确理解例题的意义：根据图形的总面积等于各个部分的面积的和，是解题的关键．
练习册系列答案
相关题目
