题目内容
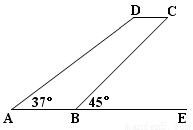
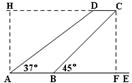
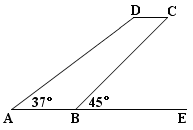
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37º,∠CBE=45º,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.
(参考数据: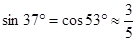 ,
,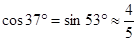 ,
,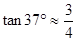 )
)
【答案】
8.5m,3m
【解析】
试题分析:作AH⊥CD于H,作CF⊥AB于F.在Rt△AHD中,根据∠ADH的正弦函数可求得AD的长,根据∠ADH的正切函数可求得DH的长,在Rt△BCF中,∠CBF=45º,根据等腰直角三角形的性质可求得BF=CF=5.1,从而可以求得结果.
作AH⊥CD于H,作CF⊥AB于F.
在Rt△AHD中,∠ADH=37º,
由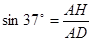 ,得
,得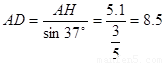 (m)
(m)
由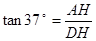 ,得
,得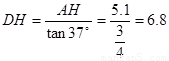
在Rt△BCF中,∠CBF=45º,所以BF=CF=5.1,
因为AB+BF=HD+DC,所以AB=6.8+1.3-5.1=3(m).
考点:解直角三角形的应用
点评:解直角三角形的应用是初中数学的重点,是中考中比较常见的知识点,一般难度不大,正确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
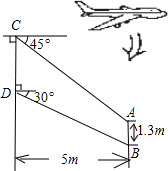 某型号飞机的机翼形状如图所示,AB∥CD,根据图中数据计算AC、BD和CD的长度(精确到0.1米,
某型号飞机的机翼形状如图所示,AB∥CD,根据图中数据计算AC、BD和CD的长度(精确到0.1米, (2012•泰州模拟)某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.
(2012•泰州模拟)某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.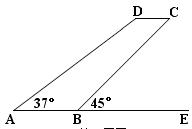
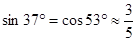 ,
,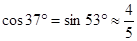 ,
,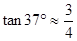 )
)
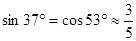 ,
,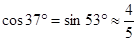 ,
,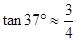 )
)
 ,
,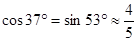 ,
,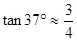 )
)