题目内容
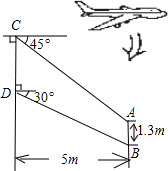 某型号飞机的机翼形状如图所示,AB∥CD,根据图中数据计算AC、BD和CD的长度(精确到0.1米,
某型号飞机的机翼形状如图所示,AB∥CD,根据图中数据计算AC、BD和CD的长度(精确到0.1米,| 2 |
| 3 |
分析:过C作CE⊥BA交BA延长线于E,在Rt△CAE中,∠ACE=45°,则△ACE是等腰直角三角形即可求得AC的长;
过B作BF⊥CD交CD延长线于F,在Rt△BFD中已知∠DBF与FB的长,利用三角函数即可求得BD的长;
根据CD=CF-FD=CE+AB-FD即可求解.
过B作BF⊥CD交CD延长线于F,在Rt△BFD中已知∠DBF与FB的长,利用三角函数即可求得BD的长;
根据CD=CF-FD=CE+AB-FD即可求解.
解答: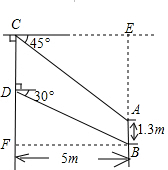 解:过C作CE⊥BA交BA延长线于E,过B作BF⊥CD交CD延长线于F(1分)
解:过C作CE⊥BA交BA延长线于E,过B作BF⊥CD交CD延长线于F(1分)
在Rt△CAE中,∠ACE=45°,∴AE=CE=5(m)(2分)
∴AC=
CE=5
≈5×1.414≈7.1(m)(3分)
在Rt△BFD中,∠DBF=30°,
∴DF=FB•tan30°
=5×
≈5×
≈2.89(m)
∴BD=2DF≈2×2.89≈5.8(m)(6分)
∴CD=1.3+5-DF≈6.3-2.89≈3.4(m)(7分)
答:AC约为7.1米,BD约为5.8米,CD约为3.4米.
 解:过C作CE⊥BA交BA延长线于E,过B作BF⊥CD交CD延长线于F(1分)
解:过C作CE⊥BA交BA延长线于E,过B作BF⊥CD交CD延长线于F(1分)在Rt△CAE中,∠ACE=45°,∴AE=CE=5(m)(2分)
∴AC=
| 2 |
| 2 |
在Rt△BFD中,∠DBF=30°,
∴DF=FB•tan30°
=5×
| ||
| 3 |
≈5×
| 1.732 |
| 3 |
∴BD=2DF≈2×2.89≈5.8(m)(6分)
∴CD=1.3+5-DF≈6.3-2.89≈3.4(m)(7分)
答:AC约为7.1米,BD约为5.8米,CD约为3.4米.
点评:此题考查了三角函数的基本概念,主要是正切函数的概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
 (2012•泰州模拟)某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.
(2012•泰州模拟)某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.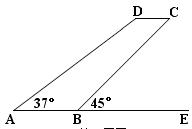
 ,
,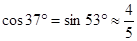 ,
,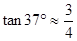 )
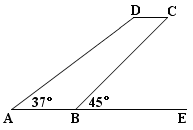
)
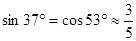 ,
,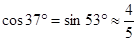 ,
,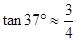 )
)
 ,
,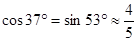 ,
,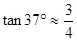 )
)