题目内容
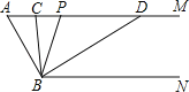
【题目】(1)如图①,在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF分别交AD、BC于点E、F,
求证:OE=OF.
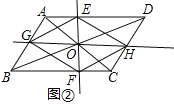
(2)在图①中,过点O作直线GH分别交AB、CD于点G、H,且满足GH⊥EF,连结EG、GF、FH、HE.如图②,试判断四边形EGFH的形状,并说明理由;
(3)在(2)的条件下,
若平行四边形ABCD变为矩形时,四边形EGFH是 ;
若平行四边形ABCD变为菱形时,四边形EGFH是 ;
若平行四边形ABCD变为正方形时,四边形EGFH是 .
【答案】(1)见解析(2)见解析(3)菱形;菱形;正方形
【解析】
试题分析:(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)若平行四边形ABCD变为矩形,即AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
若平行四边形ABCD变为菱形,即AC⊥BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
当四边形ABCD是正方形,则对角线相等且互相垂直平分;可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出EGFH的形状.
(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,
∴∠DAC=∠BCA,
在△AOE和△COF中,
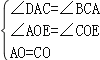 ,
,
∴△AOE≌△COF(AAS),
∴EO=FO;
(2)解:四边形EGFH是菱形;
理由:如图②:
由(1)可知,OE=OF,
同理可得:OG=OH,
∴四边形EGFH是平行四边形,
又∵EF⊥GH,
∴四边形EGFH是菱形;
(3)解:若平行四边形ABCD变为矩形时,四边形EGFH是菱形;
理由:由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
故答案为:菱形;
若平行四边形ABCD变为菱形时,四边形EGFH是菱形;
理由:由(2)知四边形EGFH是菱形,
当AC⊥BD时,对四边形EGFH的形状不会产生影响;
故答案为:菱形;
若平行四边形ABCD变为正方形时,四边形EGFH是四边形EGFH是正方形;
理由:∵四边形ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
在△BOG和△COF中
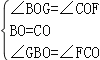 ,
,
∴△BOG≌△COF(ASA);
∴OG=OF,
同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.
故答案为:正方形.