题目内容
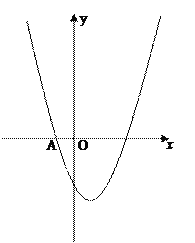
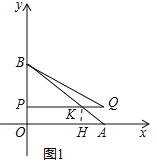
【题目】如图,在平面直角坐标系中,点O为坐标原点,三角形OAB的边OA、OB分别在x轴正半轴上和y轴正半轴上,A(a,0),a是方程![]() 的解,且△OAB的面积为6.
的解,且△OAB的面积为6.
(1)求点A、B的坐标;
(2)将线段OA沿轴向上平移后得到PQ,点O、A的对应点分别为点P和点Q(点P与点B不重合),设点P的纵坐标为t,△BPQ的面积为S,请用含t的式子表示S;
(3)在(2)的条件下,设PQ交线段AB于点K,若PK=![]() ,求t的值及△BPQ的面积.
,求t的值及△BPQ的面积.

【答案】(1)B(0,3);(2)S=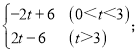 (3)4
(3)4
【解析】
(1)解方程求出a的值,利用三角形的面积公式构建方程求出b的值即可解决问题;
(2)分两种情形分别求解:当点P在线段OB上时,当点P在线段OB的延长线上时;
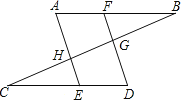
(3)过点K作KH⊥OA用H.根据S△BPK+S△AKH=S△AOB-S长方形OPKH,构建方程求出t,即可解决问题;
解:(1)∵![]() ,
,
∴2(a+2)-3(a-2)=6,
∴-a+4=0,
∴a=4,
∴A(4,0),
∵S△OAB=6,
∴![]() 4OB=6,
4OB=6,
∴OB=3,
∴B(0,3).
(2)当点P在线段OB上时,S=![]() PQPB=
PQPB=![]() ×4×(3-t)=-2t+6.
×4×(3-t)=-2t+6.
当点P在线段OB的延长线上时,S=![]() PQPB=
PQPB=![]() ×4×(t-3)=2t-6.
×4×(t-3)=2t-6.
综上所述,S=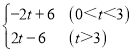 .
.
(3)过点K作KH⊥OA用H.
∵S△BPK+S△AKH=S△AOB-S长方形OPKH,
∴![]() PKBP+
PKBP+![]() AHKH=6-PKOP,
AHKH=6-PKOP,
∴![]() ×
×![]() ×(3-t)+
×(3-t)+![]() (4-
(4-![]() )t=6-
)t=6-![]() t,
t,
解得t=1,
∴S△BPQ=-2t+6=4.

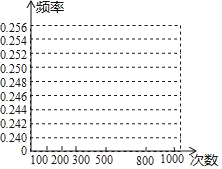
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)