Question

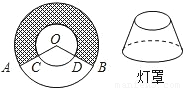
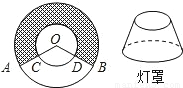
光明灯具厂生产一批台灯罩，如图的阴影部分为灯罩的侧面展开图．已知半径OA、OC分别为36cm、12cm，∠AOB=135°
（1）若要在灯罩的上下边缘镶上花边（花边的宽度忽略不计），需要多长的花边？
（2）求灯罩的侧面积（接缝不计）．（以上计算结果保留π）

Answer 1

分析：（1）主要是求阴影部分扇形环的外环和内环的弧长之和，即求优弧AB+优弧CD；直接利用弧长公式求解即可．
（2）求扇环的面积，即S_侧=S_阴影=（π×36²-S_扇形OAB）-（π×12²-S_扇形OCD）．

解答：解：（1）

AB

的长=

135π×36

180

=27π，

CD

的长=

135π×12

180

=9π，
∴花边的总长度=（2π×36-27π）+（2π×12-9π）=60π（cm）；

（2）S_扇形OAB=

135π×362

360

=486π，
S_扇形OCD=

135π×122

360

=54π，
S_侧=S_阴影=（π×36²-S_扇形OAB）-（π×12²-S_扇形OCD）=720π（cm²）．

点评：主要考查了利用弧长公式和扇形的面积公式，通过面积差求扇形的面积．