题目内容
【题目】若三角形的一边和该边上的高相等的三角形称为“和谐三角形”,如图,已知抛物线y=ax2经过A(﹣1,1),P是y轴正半轴上的动点,射线AP与抛物线交于另一点B,当△AOP是“和谐三角形”时,点B的坐标为 . 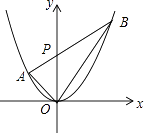
【答案】(2,4)和(1,1)
【解析】解:把A(﹣1,1)代入y=ax2得a=1,
∴抛物线解析式为y=x2,
∵A(﹣1,1),
∴∠AOP=45°,OA= ![]() ,
,
∵△AOP是“和谐三角形,
∴当点A到OP的距离等于OP时,即OP=1,此时AP⊥y轴,点A与点B关于y轴对称,则B(1,1);
当点P到OA的距离等于OA时,即点P到OA的距离等于 ![]() ,则OP=2,
,则OP=2,
此时直线AP的解析式为y=x+2,解方程x2=x+2得x1=﹣1,x2=2,则B(2,4);
同样当点O到OP的距离等于AP时,得到OP=1或OP=2.
综上所述,点B的坐标为(2,4)和(1,1).
所以答案是(2,4)和(1,1)
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目