题目内容
【题目】如图,已知点O (0,0),A (-5,0),B (2,1),抛物线 ![]() (h为常数)与y轴的交点为C。
(h为常数)与y轴的交点为C。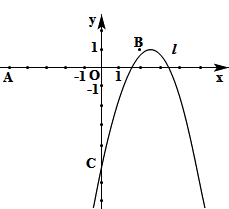
(1)抛物线经过点B,求它的解析式,并写出此时抛物线的对称轴及顶点坐标;
(2)设点C的纵坐标为 ![]() ,求
,求 ![]() 的最大值,此时抛物线上有两点
的最大值,此时抛物线上有两点 ![]() ,
, ![]() ,其中
,其中 ![]() ,比较
,比较 ![]() 与
与 ![]() 的大小;
的大小;
(3)当线段OA被只分为两部分,且这两部分的比是1:4时,求h的值。
【答案】
(1)解:把 ![]() 代入
代入 ![]() ,得:
,得: ![]() ,
,
∴解析式为: ![]() (或
(或 ![]() ).
).
∴对称轴为: ![]() ,顶点
,顶点 ![]()
(2)解:点 ![]() 的横坐标为0,则
的横坐标为0,则 ![]() ,
,
∴当 ![]() 时,
时, ![]() 有最大值为1.
有最大值为1.
此时,抛物线为: ![]() ,对称轴为:
,对称轴为: ![]() (y轴),
(y轴),
当 ![]() ≥
≥ ![]() 时,
时, ![]() 随着
随着 ![]() 的增大而减小,
的增大而减小,
∴ ![]() >
> ![]() ≥
≥ ![]() 时,
时, ![]() <
< ![]()
(3)解:把线段OA分1:4两部分的点是 ![]() 或
或 ![]() ,
,
把 ![]() 代入
代入 ![]() ,得:
,得: ![]() 或
或 ![]() .
.
但 ![]() 时,线段OA被分为三部分,不合题意,舍去.
时,线段OA被分为三部分,不合题意,舍去.
同样,把 ![]() 代入
代入 ![]() ,
,
得: ![]() 或
或 ![]() (舍去)
(舍去)
∴ ![]() 的值为
的值为 ![]() 或
或 ![]()
【解析】(1)将点B的坐标代入函数解析式即可求出答案。
(2)根据已知点C在y轴上,得出yc=h2+1 ,由于最大值为yc,因此可知h=0时,最大值为1,此时抛物线的解析式为y=x2+1 ,根据二次函数的性质,可知当 x ≥ 0 时, y 随着 x 的增大而减小,即可得出结论。
(3)根据题意可知把线段OA分1:4两部分的点是 ( 1 , 0 ) 或 ( 4 , 0 ) ,将这两点坐标分别代入函数解析式,即可求出符合条件的h的值。

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目