题目内容
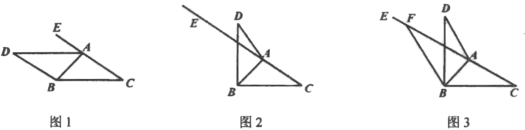
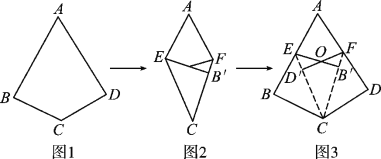
【题目】阅读理解:如图1,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状,再展开得到图3,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图3中的∠BCD=120°时,∠AEB′= ;
拓展提升:
(3)当图2中的四边形AECF为菱形时,对应图3中的四边形CD′OB′是否是“完美筝形”?请说明理由.
【答案】(1)正方形;(2)80°;(3)四边形CD′OB′是“完美筝形”,理由详见解析.
【解析】
(1)根据“完美风筝”的定义判断即可得到结果;
(2)根据根据∠BCE=∠ECF=∠FCD,可得到∠BCE=![]() ∠BCD=40°,由三角形的内角和可得∠BEC=50°,根据对折得到∠BEC=∠B′EC,根据邻补角即可求解;
∠BCD=40°,由三角形的内角和可得∠BEC=50°,根据对折得到∠BEC=∠B′EC,根据邻补角即可求解;
(3)根据“完美筝形”的定义得出线段、角相等,转化到四边形ODCB中,即可.
解:(1)∵若四边形ABCD是正方形,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴正边形一定是“完美筝形”
(2)由对折有,∠BEC=∠B′EC,
∵∠BCE=∠ECF=∠FCD,且∠BCD=120°,
∴∠BCE=![]() ∠BCD=40°,
∠BCD=40°,
∴∠BEC=90°﹣∠BCE=50°,
∴∠BEB′=100°
∴∠AEB′=80°,
(3)四边形CD′OB′是“完美筝形”.
理由:∵四边形ABCD是“完美筝形”,
∴CB=CD,∠B=∠D=90°.
由折叠可知,CD′=CD,CB′=CD,∠CD′O=∠CB′O=90°,
∴CD′=CB′,∠OD′E=∠OB′F=90°.
∵四边形AECF为菱形,
∴CE=CF,
∴D′E=B′F,
在△OED′和△OFB′中,
∴△OED′≌△OFB′(AAS),
∴OD′=OB′,
∴四边形CD′OB′是“完美筝形”.
故答案为:(1)正方形;(2)80°;(3)四边形CD′OB′是“完美筝形”,理由详见解析.

 阅读快车系列答案
阅读快车系列答案