��Ŀ����
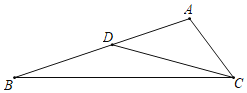
����Ŀ����֪����ͼ����ABC����BDE���ǵ���ֱ�������Σ���ACB����BDE��90������F��AE���е㣬����DF��CF��
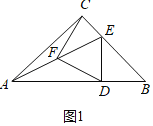
��1����ͼ1����D��E�ֱ���AB��BC���ϣ���գ�CF��DF��������ϵ���� ����λ�ù�ϵ���� ����
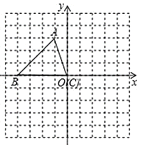
��2����ͼ2����ͼ1�е���BDE��B˳ʱ����ת45���õ�ͼ2�����жϣ�1����CF��DF��������ϵ��λ�ù�ϵ�Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�
��3����ͼ3����ͼ1�е���BDE��B˳ʱ����ת90���õ�ͼ3�����BD��2��AC��3![]() ����ֱ��д��CF�ij���
����ֱ��д��CF�ij���

���𰸡���1��CF��DF��CF��DF����2��������֤������������3��![]() ��
��
��������
��1����ͼ1�У����ۣ�CF��DF��CF��DF������ֱ�������ε�б�����ߵ����ʼ��ɽ�����⣮
��2����������ͼ2�У��ӳ�DF��AC��H��֤����AFH�ա�EFD��ASA�������ɽ�����⣮
��3����ͼ3�У��ӳ�DF��AB��H������CH��CD��֤����AFH�ա�EFD��ASA�����Ƴ�DF��FH��AH��DE��DB����֤����CAH�ա�CBD��SAS�������ɽ�����⣮
�⣺��1�����ۣ�CF��DF��CF��DF��
���ɣ���ͼ1�У�
�ߡ�ACE��ADE��90����AF��FE��
��CF��AF��FE��![]() AE��DF��AF��FE��
AE��DF��AF��FE��![]() AE��
AE��
��CF��DF��
���FAC����FCA����FAD����FDA��
��CA��CB����ACB��90����
���CAB��45����
�ߡ�CFE����FAC+��FCA��2��FAC����EFD����FAD+��FDA��2��FAD��
���CFD����CFE+��EFD��2����FAC+��FAD����2��CAD��90����
��CF��DF��
�ʴ�Ϊ��CF��DF��CF��DF��
��2��������
���ɣ���ͼ2�У��ӳ�DF��AC��H��
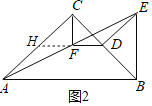
�ߡ�ACD����BDE����CDE��90����
��AC��DE��
���FED����FAH��
�ߡ�AFH����EFD��FA��FE��
���AFH�ա�EFD��ASA����
��DF��FH��
�ߡ�HCD��90����
��CF��FH��FD��CF��DF��
��3����ͼ3�У��ӳ�DF��AB��H������CH��CD��
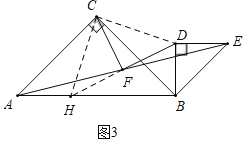
�ߡ�ABD����CDE��90����
��DE��AB��
���FED����FAH��
�ߡ�AFH����EFD��FA��FE��
���AFH�ա�EFD��ASA����
��DF��FH��AH��DE��DB��
�ߡ�CAH����CBA����CBD��45����CA��CB��
���CAH�ա�CBD��SAS����
��CH��CD����ACH����BCD��
���HCD����ACB��90������FH��FD��
��CF��DF��CF��FH��DF��
��AC��CB��3![]() ��
��
��AB��![]() AC��6��
AC��6��
��AH��BD��2��
��BH��6��2��4��
��Rt��BDH��DH��![]() ��2
��2![]() ��
��
��CF��DF��FH��![]() ��
��

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�����Ŀ���������������������أ�����ij�����̳Ǹ������ڽ�������������ij�ּ��ÿ������������������200Ԫ/̨.�����г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1��������б���ֱ��д����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ���ۼ�x��ȡֵ��Χ��
�ۼۣ�Ԫ/̨�� | ����������̨�� |
400 | 200 |
250 | |
x |
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�