题目内容
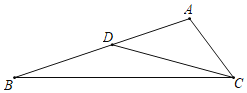
【题目】如图,已知在△ABC中,点D在AB上,BD=CD=3,AD=2,∠ACB=60°,那么AC的长等于_____.
【答案】![]() .
.
【解析】
如图,过点A作AE⊥BC于点E,作DF⊥BC于点F,则DF∥AE,设EC=x,BF=y,分别用x和y表示出AC、AE、BF、CF和BE,再由DF∥AE,判定△BDF∽△BAE,然后利用相似三角形的性质得出比例式,解得用x表示的BE,在Rt△AEB中,AB=5,AE=![]() x,BE=5x,由勾股定理得关于x的方程,解得x的值,则可求得AC的值.
x,BE=5x,由勾股定理得关于x的方程,解得x的值,则可求得AC的值.
解:如图,过点A作AE⊥BC于点E,作DF⊥BC于点F,则DF∥AE,
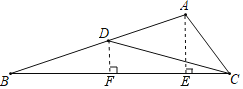
∵∠ACB=60°,
∴∠CAE=30°,
设EC=x,则AC=2x,AE=![]() x,
x,
设BF=y,
∵BD=CD,DF⊥BC,
∴BF=CF=y,
∴BE=2y﹣x,
∵DF∥AE,
∴△BDF∽△BAE,
∴![]() =
=![]() ,
,
∵BD=CD=3,AD=2,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]()
∴y=3x,
∴BE=2×3x﹣x=5x,
∴在Rt△AEB中,AB=5,AE=![]() x,BE=5x,
x,BE=5x,
∴由勾股定理得:BE2+AE2=AB2,
∴25x2+3x2=25,
∴x2=![]() ,
,
∵x>0,
∴x=![]() ,
,
∴AC=2x=![]() .
.
故答案为:![]() .
.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为![]() (单位:km),乘坐地铁的时间
(单位:km),乘坐地铁的时间![]() (单位:min)是关于
(单位:min)是关于![]() 的一次函数,其关系如下表:
的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x/km | 7 | 9 | 11 | 12 | 13 |
y1/min | 16 | 20 | 24 | 26 | 28 |
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)李华骑单车的时间![]() (单位:min)也受
(单位:min)也受![]() 的影响,其关系可以用
的影响,其关系可以用![]() =
=![]()
![]() 2-11
2-11![]() +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
+78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.