题目内容
【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
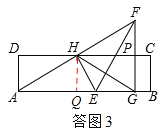
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

【答案】(1)①45;②当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() ;(2)
;(2)![]() .
.
【解析】
(1)①∵四边形ABCD是矩形,∴∠ADH=90°.
∵DH=DA,∴∠DAH=∠DHA=45°.∴∠HAE=45°.
∵HA=HG,∴∠HAE=∠HGA=45°
②分两种情况讨论:
第一种情况:如答图1,∠AHE为锐角时,
∵∠HAG=∠HGA=45°,∴∠AHG=90°.
由折叠可知:∠HAE=∠F=45°,∠AHE=∠FHE,
∵EF∥HG,∴∠FHG=∠F=45°.
∴∠AHF=∠AHG![]() ∠FHG=45°,即∠AHE+∠FHE=45°.
∠FHG=45°,即∠AHE+∠FHE=45°.
∴∠AHE=22.5°.
此时,当B与G重合时,a的值最小,最小值是2.

第二种情况:如答图2,∠AHE为钝角时,
∵EF∥HG,∴∠HGA=∠FEA=45°,即∠AEH+∠FEH=45°.
由折叠可知:∠AEH=∠FEH,∴∠AEH=∠FEH=22.5°.
∵EF∥HG,∴∠GHE=∠FEH=22.5°.
∴∠AHE=90°+22.5°=112.5°.
此时,当B与E重合时,a的值最小,
设DH=DA=x,则AH=CH=![]() x,
x,
在Rt△AHG中,∠AHG=90°,由勾股定理得:AG=![]() AH=2x,
AH=2x,
∵∠AEH=∠FEH,∠GHE=∠FEH,∴∠AEH=∠GHE.∴GH=GE=![]() x.
x.
∴AB=AE=2x+![]() x.
x.
∴a的最小值是![]() .
.
综上所述,当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() .
.

(2)如答图3:过点H作HQ⊥AB于Q,则∠AQH=∠GQH=90°,
在矩形ABCD中,∠D=∠DAQ=90°,
∴∠D=∠DAQ=∠AQH=90°.
∴四边形DAQH为矩形.∴AD=HQ.
设AD=x,GB=y,则HQ=x,EG=2y,
由折叠可知:∠AEH=∠FEH=60°,∴∠FEG=60°.
在Rt△EFG中,EG=EF×cos60°=2y,
在Rt△HQE中,![]() ,
,
∴![]() .
.
∵HA=HG,HQ⊥AB,∴AQ=GQ=![]() .
.
∴AE=AQ+QE=![]() .
.
由折叠可知:AE=EF,即![]() ,即
,即![]() .
.
∴AB=2AQ+GB= .
.
∴ .
.