题目内容
【题目】定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形。
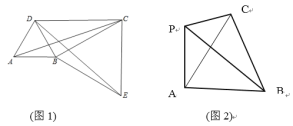
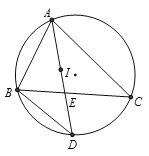
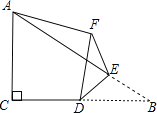
(1)如图1,将△ABC绕顶点B按顺时针方向旋转60得到△DBE,∠DCB=30,连接AD,DC,CE
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形。
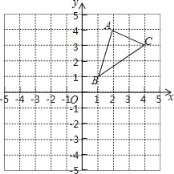
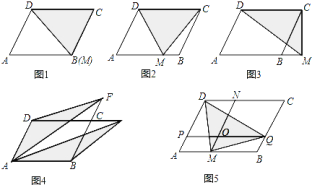
(2)如图2已知等边ABC的边长等于4平面上存在一点P若使四边形PABC形成勾股四边形且PC=2,PA,PC不能同时成为一组勾股边,直接写出此时PBC的面积。
【答案】(1)见解析;(2)7.
【解析】
(1) ①由旋转的性质可知△ABC≌△DBE,从而可得BC=BE,由∠CBE=60°可得△BCE为等边三角形;②由①可得∠BCE=60°,从而可知△DCE是直角三角形,再利用勾股定理即可解决问题.
(2)根据题意可知BC和BA应组成勾股边,由此计算出PB的平方的值,过点B做PC延长线上的垂线,垂足为D,设DC=x,在△PBD中根据勾股定理可计算出x的值,即可求出BD的长度,以PC为底,BD为高即可求出PBC的面积.
(1)①∵△ABC绕点B顺时针旋转了60°到△DBE,
∴BC=BE,∠CBE=60°,
∵在△BCE中,BC=BE,∠CBE=60°
∴△BCE是等边三角形.
②∵△BCE是等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=90°,
在Rt△DCE中,有DC2+CE2=DE2,
∵DE=AC,BC=CE,
∴DC2+BC2=AC2,
∴四边形ABCD是勾股四边形.
(2)②如图,
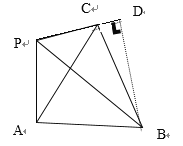
∵由条件已知PC和PA,PA和BA,PC和BC无法组成勾股边
∴若使四边形PABC形成勾股四边形
∴BC和BA应组成勾股边
∴PB2=BC2+BA2=32
如图过点B做PC延长线上的垂线,垂足为D
设CD为x,则BD2=16-x2
∵PB2=(PC+CD)2+BD2
∴32=(2+x)2+16-x2
解得x=3
∴BD=7
∴SPBC=2×7×![]() =7
=7
则PBC的面积为7.