��Ŀ����
��֪���κ���y=a��x+p��2+4��ͼ�����ɺ���y=
x2+2x+q��ͼ������ƽ��һ����λ�õ�������������y=
����κ���y=a��x+p��2+4��ͼ���ڵ�A��1��n����
��1����a��p��q��m��n��ֵ��
��2��Ҫʹ�����������Ͷ��κ���y=a��x+p��2+4��ֱ��x=t��һ���y����x���������С����t�����ֵ��
��3���Ƕ��κ���y=a��x+p��2+4ͼ��Ķ���ΪB����ABΪ�߹������ABCD����CD�뺯��y=
�ཻ����ֱ��AB��CD�ľ���Ϊ
�������D��C�����꣮
| 1 |
| 2 |
| m |
| x |
��1����a��p��q��m��n��ֵ��
��2��Ҫʹ�����������Ͷ��κ���y=a��x+p��2+4��ֱ��x=t��һ���y����x���������С����t�����ֵ��
��3���Ƕ��κ���y=a��x+p��2+4ͼ��Ķ���ΪB����ABΪ�߹������ABCD����CD�뺯��y=
| m |
| x |
| 5 |
��������1���Ƚ�����y=
x2+2x+q�䷽�����ɵõ��������꣨-2��q-2��������ƽ�Ƶ����ʿɵ�a=
��p=3��q=6���ٰ�x=1��y=n����y=
(x+3)2+4����x=1��y=12����y=
����m��n��ֵ��
��2�����ݷ����������������ԣ����κ���y=
(x+3)2+4�ĶԳ���������ԣ��������t�����ֵ��
��3������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E�������ݹ��ɶ��������ε����ʣ����������ε��ж������ʣ�������õ�D��C�����꣮
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| x |
��2�����ݷ����������������ԣ����κ���y=
| 1 |
| 2 |
��3������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E�������ݹ��ɶ��������ε����ʣ����������ε��ж������ʣ�������õ�D��C�����꣮
����⣺��1��y=
x2+2x+q=
(x2+4x)+q=
(x+2)2+q-2���������꣨-2��q-2��
�����ö������깫ʽ��
��a=
��p=3��q=6��
��x=1��y=n����y=
(x+3)2+4��n=12��
��x=1��y=12����y=
��m=12��
��2���߷���������y=
��ͼ�����ڵ�ÿһ�����ڣ�y����x���������С
�������y=
(x+3)2+4�ĶԳ���Ϊ��ֱ��x=-3
Ҫʹ���κ���y=
(x+3)2+4��������������x��-3
��t�����ֵΪ-3��
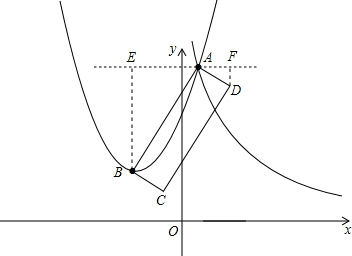 ��3����ͼ������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E��
��3����ͼ������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E��
�ߵ�B������Ϊ��-3��4����A��1��12��
��AE=4��BE=8
��BE��l��
��AB=
=4
��
���ı���ABCD�Ǿ��Σ�
���BAD=90�㣬
���EAB+��FAD=90��
��BE��l��E��
���EAB+��EBA=90��
���FAD=��EBA
��Rt��EBA��Rt��FAD
��
=
�֡�AD=
��
��FD=1
ͬ����AF=2
���D��������3��11��
ͬ�������C��-1��3����
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�����ö������깫ʽ��
��a=
| 1 |
| 2 |
��x=1��y=n����y=
| 1 |
| 2 |
��x=1��y=12����y=
| m |
| x |
��2���߷���������y=
| 12 |
| x |
�������y=
| 1 |
| 2 |
Ҫʹ���κ���y=
| 1 |
| 2 |
��t�����ֵΪ-3��
 ��3����ͼ������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E��
��3����ͼ������A��ֱ��l��x�ᣬ��DF��l��F��BE��l��E���ߵ�B������Ϊ��-3��4����A��1��12��
��AE=4��BE=8
��BE��l��
��AB=
| AE2+BE2 |
| 5 |
���ı���ABCD�Ǿ��Σ�
���BAD=90�㣬
���EAB+��FAD=90��
��BE��l��E��
���EAB+��EBA=90��
���FAD=��EBA
��Rt��EBA��Rt��FAD
��
| AB |
| AE |
| AD |
| FD |
�֡�AD=
| 5 |
��FD=1
ͬ����AF=2
���D��������3��11��
ͬ�������C��-1��3����
�����������˶��κ����ۺ��⣬�漰��֪ʶ���У��䷽����Ӧ�ã�ƽ�Ƶ����ʣ������������������ԣ����κ����������ԣ����ɶ��������ε����ʣ����������ε��ж������ʣ��ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
�����Ŀ
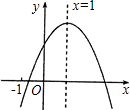 ��2013•�����ض�ģ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ�
��2013•�����ض�ģ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ�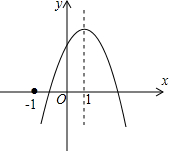 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���ac��0����a-b+c��0��
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���ac��0����a-b+c��0��