题目内容
矩形ABCO的面积为10,OA比OC大3,E为BC的中点,以OE为直径的⊙O′交x轴于D,DF⊥AE于F.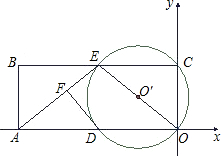
(1)求OA、OC的长.
(2)求DF长;
(3)P为边BC上一动点,设△ABP的面积为x,△OPC的面积为y,求y与x的函数关系式,并写出x的取值范围.
(4)直线BC上是否存在点Q,使∠AQO=90°?若存在,求出Q点坐标;若不存在,请说明理由.
分析:(1)设出OC的长为x,表示出OA=x+3,根据矩形的面积公式列出关于x的方程,求出方程的解得到x的值,即可求出OA和OC的长;
(2)由E为BC的中点,得到点D为AD中点,在直角三角形ABE中,根据勾股定理求出AE的长,然后利用两对角相等证明△ABE∽△DFA,根据相似三角形的对应边成比例即可求出DF的长;
(3)由矩形的面积等于三角形AED面积的2倍,得到三角形ABP的面积与三角形OCP的面积之和为5,即可列出y关于x的函数关系式,进而求出x的取值范围;
(4)存在.根据题意画出图形,由AQ与QD垂直得到角AQB与角CQD互余,又角AQB与角BAQ互余,根据同角的余角相等得到角CQD与角BAQ相等,又角B与角DCQ相等都等于直角,所以得到△ABQ与QCD两三角形相似,设BQ=a,则QC=5-a,根据相似三角形对应边成比例列出关于a的方程,求出a的值即可得到点Q的坐标.
(2)由E为BC的中点,得到点D为AD中点,在直角三角形ABE中,根据勾股定理求出AE的长,然后利用两对角相等证明△ABE∽△DFA,根据相似三角形的对应边成比例即可求出DF的长;
(3)由矩形的面积等于三角形AED面积的2倍,得到三角形ABP的面积与三角形OCP的面积之和为5,即可列出y关于x的函数关系式,进而求出x的取值范围;
(4)存在.根据题意画出图形,由AQ与QD垂直得到角AQB与角CQD互余,又角AQB与角BAQ互余,根据同角的余角相等得到角CQD与角BAQ相等,又角B与角DCQ相等都等于直角,所以得到△ABQ与QCD两三角形相似,设BQ=a,则QC=5-a,根据相似三角形对应边成比例列出关于a的方程,求出a的值即可得到点Q的坐标.
解答:解:(1)设OC=x,则OA=x+3,
由题意得:x(x+3)=10,
即(x-2)(x+5)=0,
解得:x=2,x=-5(舍去),
∴OA=5,OC=2;
(2)∵E为BC的中点,得到D为AD中点,且BC=5,AB=2,
∴AD=BE=2.5,根据勾股定理得:AE=
=
,
∵矩形ABCD,∴BC∥AD,
∴∠BEA=∠EAD,又∠B=∠AFD=90°,
∴△ABE∽△DFA,
∴
=
,
则DF=
;
(3)∵S矩形ABCD=S△AED,
∴S△ABP+S△OCP=
S矩形ABCD,即x+y=5,
则y=5-x(0<x<5);
(4)存在.画出图形,如图所示:
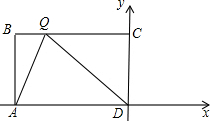 当AQ⊥QO时,∠AQB+∠CQD=90°,
当AQ⊥QO时,∠AQB+∠CQD=90°,
∵∠AQB+∠BQA=90°,
∴∠CQD=∠BAQ,
又∠B=∠DCQ=90°,
∴△ABQ∽△QCD,∴
=
,设BQ=a,则QC=5-a,
∴
=
,即(a-1)(a-4)=0,
解得:a=1或a=4,
当BQ=a=1时,点Q坐标为(-4,2);
当BQ=a=4时,点Q坐标为(-1,2),
综上,Q坐标为(-1,2)或(-4,2).
由题意得:x(x+3)=10,
即(x-2)(x+5)=0,
解得:x=2,x=-5(舍去),
∴OA=5,OC=2;
(2)∵E为BC的中点,得到D为AD中点,且BC=5,AB=2,
∴AD=BE=2.5,根据勾股定理得:AE=
| 22+2.52 |
| ||
| 2 |
∵矩形ABCD,∴BC∥AD,
∴∠BEA=∠EAD,又∠B=∠AFD=90°,
∴△ABE∽△DFA,
∴
| AB |
| DF |
| AE |
| AD |
则DF=
10
| ||
| 41 |
(3)∵S矩形ABCD=S△AED,
∴S△ABP+S△OCP=
| 1 |
| 2 |
则y=5-x(0<x<5);
(4)存在.画出图形,如图所示:
 当AQ⊥QO时,∠AQB+∠CQD=90°,
当AQ⊥QO时,∠AQB+∠CQD=90°,∵∠AQB+∠BQA=90°,
∴∠CQD=∠BAQ,
又∠B=∠DCQ=90°,
∴△ABQ∽△QCD,∴
| BQ |
| CD |
| AB |
| QC |
∴
| a |
| 2 |
| 2 |
| 5-a |
解得:a=1或a=4,
当BQ=a=1时,点Q坐标为(-4,2);
当BQ=a=4时,点Q坐标为(-1,2),
综上,Q坐标为(-1,2)或(-4,2).
点评:此题考查了同学们利用三角形相似的判断与性质、直角三角形的性质以及一元二次方程的应用等知识解决问题的能力,有利于培养同学们的发散思维能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F. 19、如图,在平面直角坐标系中,矩形ABCO的面积为15,且OA=OC+2,E为BC的中点,以OE为直径的⊙O′交y轴于D点,过D作DF⊥AE于点F.
19、如图,在平面直角坐标系中,矩形ABCO的面积为15,且OA=OC+2,E为BC的中点,以OE为直径的⊙O′交y轴于D点,过D作DF⊥AE于点F.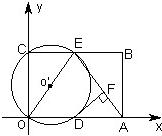 29、如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交X轴于D点,过D点作DF⊥AE于F.
29、如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交X轴于D点,过D点作DF⊥AE于F. 如图,点B是反比例函数y=-
如图,点B是反比例函数y=-