题目内容
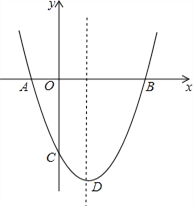
【题目】如图,抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点D为抛物线的顶点.
,点D为抛物线的顶点.
![]() 求抛物线解析式和顶点D的坐标;
求抛物线解析式和顶点D的坐标;
![]() 求抛物线与x轴的两交点A、B的坐标;
求抛物线与x轴的两交点A、B的坐标;
![]() 你可以直接写出不等式
你可以直接写出不等式![]() 的解集吗?
的解集吗?
【答案】(1)顶点D的坐标为![]() ;(2)
;(2)![]() 、B的坐标分别为
、B的坐标分别为![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)把点C(0,-3)代入解析式可得c=-3,由对称轴为直线x=![]() 可解得b=-2,由此即可得到抛物线的解析式;再把所得解析式配方化为“顶点式”,即可得到顶点坐标;
可解得b=-2,由此即可得到抛物线的解析式;再把所得解析式配方化为“顶点式”,即可得到顶点坐标;
(2)由二次函数解析式中y=0,解得对应的x的值,即可求得A、B两点的坐标;
(3)由(2)中所求A、B的坐标结合抛物线开口向上即可得到不等式![]() 的解集.
的解集.
试题解析:
(1)∵抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,
∴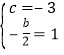 ,解得:b=-2,c=3,
,解得:b=-2,c=3,
∴抛物线的解析式为:y=x2-2x-3,
∵y=x2-2x+3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4);
(2)在y=x2-2x-3中,当y=0时,x2-2x-3=0,解得:x1=3,x2=-1,
∴A的坐标为(-1,0),B的坐标为(3,0);
(3)∵A的坐标为(-1,0),B的坐标为(3,0),抛物线y=x2-2x-3开口向上,
∴![]() 的解集为:
的解集为:![]() .
.

练习册系列答案
相关题目