题目内容
【题目】探究题：已知：如图,
,
.求证：
.
老师要求学生在完成这道教材上的题目证明后，尝试对图形进行变形，继续做拓展探究，看看有什么新发现？
（1）小颖首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小颖用到的平行线性质可能是 .
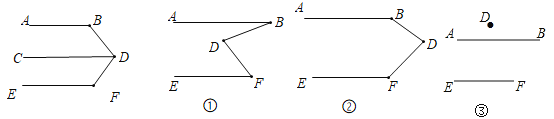
（2）接下来，小颖用《几何画板》对图形进行了变式，她先画了两条平行线
，然后在平行线间画了一点
，连接
后，用鼠标拖动点，分别得到了图
，小颖发现图
正是上面题目的原型，于是她由上题的结论猜想到图和
图中的与
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能，找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上，继续完成下面的问题：
（ⅰ）猜想图中与
之间的数量关系并加以证明；
（ⅱ）补全图，直接写出与之间的数量关系： .
【答案】（1）两直线平行同旁内角互补；（2）（ⅰ）
，见解析；（ⅱ）见解析，
.
【解析】
（1）根据两直线平行同旁内角互补即可解决问题；
（2）（ⅰ）猜想∠BDF=∠B+∠F．过点D作CD∥AB．利用平行线的性质即可解决问题；
（ⅱ）∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF．利用平行线的性质已经三角形的外角的性质即可解决问题；
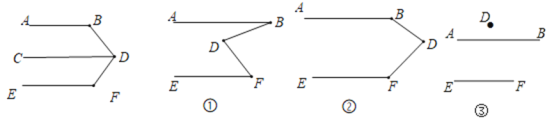
解：（1）∵AB//CD，
∴∠B+∠BDC=180°(两直线平行，同旁内角互补)，
∵CD//EF(已知)，
∴∠CDF+∠DFE=180°(两直线平行，同旁内角互补)，
∴∠B+∠BDF+∠F=∠B+∠BDC+∠CDF+∠DFE=360°．
故答案为:两直线平行同旁内角互补．
(2)（ⅰ）猜想
证明：过点
作
，
,
（ⅱ）补全图形如图所示：∠B、∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF．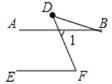
理由：∵AB∥EF，
∴∠1=∠F，
∵∠1=∠B+∠D，
∴∠F=∠B+∠BDF．
故答案为∠F=∠B+∠BDF．
