Question

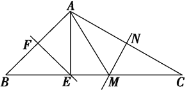
【题目】如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的垂直平分线，E、M在BC上，则∠EAM等于 ( )

A. 58° B. 32°

C. 36° D. 34°

Answer 1

【答案】B

【解析】

先由∠BAC=106°及三角形内角和定理求出∠B+∠C的度数，再根据线段垂直平分线的性质求出∠B=∠BAE，∠C=∠CAN，即∠B+∠C=∠BAE+∠CAN，由∠EAN=∠BAC-（∠BAE+∠CAN）解答即可．

∵△ABC中,∠BAC=106°，

∴∠B+∠C=180°∠BAC=180°106°=74°，

∵EF、MN分别是AB、AC的中垂线，

∴∠B=∠BAE，∠C=∠CAN，

即∠B+∠C=∠BAE+∠CAN=74°，

∴∠EAN=∠BAC(∠BAE+∠CAN)=106°74°=32°.

故答案为B.