题目内容
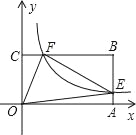
【题目】如图,平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴的正半轴上,反比例函数y=![]() 在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F,已知BE=2AE,四边形的OEBF的面积等于12.
在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F,已知BE=2AE,四边形的OEBF的面积等于12.
(1)求k的值;
(2)若射线OE对应的函数关系式是y=![]() ,求线段EF的长;
,求线段EF的长;
(3)在(2)的条件下,连结AC,试证明:EF∥AC.
【答案】(1)k的值为6;(2)EF![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)由△OAE面积与k的关系可求得k值;
(2)由于点E为两函数的交点,联立方程可求得点E的坐标,进而求出点B、F的坐标,由勾股定理即可求出EF的长;
(3)易证△BEF∽△BAC,从而得到∠BEF=∠BAC,进而得到两直线平行.
(1)连接OB,如图1所示,

∵S△OAB=S△OCB,S△OCF=S△OAE=![]() ,
,
∴S△OFB=S△OBE,
∵S△OFB+S△OBE=12,
∴S△OBE=6,
∵BE=2AE,
∴S△OBE=2S△OAE=6,
∴S△OAE=![]() =3,
=3,
∴k=6,
∴k的值为6;
(2)解方程![]() ,得x=±6,
,得x=±6,
∵点E在第一象限,
∴x=6,
把x=6代入![]() ,
,
得y=1,即点E(6,1).
∵BE=2AE,
∴点B(6,3),
把y=3代入![]() ,得x=2.
,得x=2.
∴点F(2,3),
∴BF=6﹣2=4,BE=3﹣1=2,
在直角△BEF中,根据勾股定理得:![]() ;
;
(3)连接AC,如图2所示,

∵BF=4,BE=2,BC=6,BA=3,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠B=∠B,
∴△BEF∽△BAC,
∴∠BEF=∠BAC.
∴EF∥AC.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目