题目内容
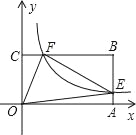
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在坐标轴上,
在坐标轴上,![]() 是
是![]() 的中点,四边形
的中点,四边形![]() 是矩形,四边形
是矩形,四边形![]() 是正方形,若点
是正方形,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
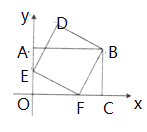
过点D作DH⊥y轴,交y轴于H,根据矩形和正方形的性质可得∠EOF=∠BCF=∠HDE=90°,EF=BF=ED,BC=OA,根据角的和差故关系可得∠FBC=∠OFE=∠HED,∠BFC=∠OEF=∠HDE,利用ASA可证明△OFE≌△CBF≌△HDE,可得FC=OE=HD,BC=OF=HE,由点E为OA中点可得OF=2FC,即可求出FC的长,进而可得HE的长,即可求出OH的长,即可得点D坐标.
过点D作DH⊥y轴,交y轴于H,
∵四边形![]() 是矩形,四边形
是矩形,四边形![]() 是正方形,
是正方形,
∴∠EOF=∠BCF=∠HDE=∠EFB=90°,EF=BF=ED,BC=OA,
∴∠OFE+∠BFC=90°,∠FBC+∠BFC=90°,
∴∠OFE=∠FBC,
同理:∠OEF=∠BFC,
在△OEF和△CFB中,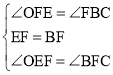 ,
,
∴BC=OF=OA,FC=OE,
∵点E为OA中点,
∴OA=2OE,
∴OF=2OE,
∴OC=3OE,
∵点C坐标为(3,0),
∴OC=3,
∴OE=1,OF=2,
同理:△HDE≌△OEF,
∴HD=OE=1,HE=OF=2,
∴OH=OE+HE=3,
∴点D坐标为(1,3),

故选:D.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目