题目内容
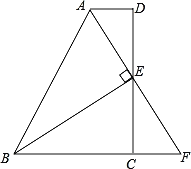
【题目】已知：如图，直线
与
轴、
轴分别交于
、
两点，两动点
、
分别以
个单位长度/秒和
个单位长度/秒的速度从、两点同时出发向
点运动（运动到点停止）；过点作
交抛物线
于、
两点，交
于点
，连结
、
．若抛物线的顶点
恰好在上且四边形
是菱形，则
、
的值分别为（ ）
A. 
、
B. 、
C. 
、 D. 、
【答案】A
【解析】
首先求出一次函数
与坐标轴交点A、B的坐标，由EF∥AD，且EF=AD=t，则四边形ADEF为平行四边形，若平行四边形ADEF是菱形，则DE=AD=t．由DE=2OD，列方程求出t的值，进而得出G、E点坐标，求出直线BG的解析式，即可得出M点坐标，进而得出a、h的值．
在直线解析式中，令x=0，得y=
3；令y=0，得x=1，
∴A（1，0），B（0，），OA=1，OB=，
∴AB=
=2，
∴∠OBA=30°，
∴BF=2EF，
∵BE=
，BF2=EF2+BE2，
∴EF=t，
∵EF∥AD，且EF=AD=t，
∴四边形ADEF为平行四边形，
若平行四边形ADEF是菱形，则DE=AD=t，
由DE=2OD，即：t=2（1-t），解得：t=
，
∴t=时，四边形ADEF是菱形，
此时BE=
，则E（0，
），G（2，），
设直线BG的解析式为：y=kx+b，将（0，），（2，）代入得：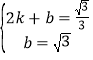
，
解得：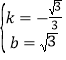
，
故直线BG的解析式为：y=-x+，
当x=1时，y=，即M点坐标为（1，），
故抛物线y=a（x-1）2+，
将（0，）代入得：a=-，
则a、h的值分别为：
、，
故选A．
【题目】随着车辆的增加，交通违规的现象越来越严重，交警对某雷达测速区检测到的一组汽车的时速数据进行整理，得到其频数及频率如表（未完成）：
数据段 | 频数 | 频率 |
30～40 | 10 | 0.05 |
40～50 | 36 | |
50～60 | 0.39 | |
60～70 | ||
70～80 | 20 | 0.10 |
总计 | 200 | 1 |
注：30～40为时速大于等于30千米而小于40千米，其他类同
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？
