题目内容
【题目】如图,Rt△ABC中,∠ACB=90°.
(1)作∠BAC的平分线,交BC于点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BD=5,CD=3,求AC的长.
【答案】(1)见解析;(2)6.
【解析】
(1)先以A为圆心,小于AC长为半径画弧,交AC,AB运用H、F;再分别以H、F为圆心,大于![]() HF长为半径画弧,两弧交于点M,最后画射线AM交CB于D;
HF长为半径画弧,两弧交于点M,最后画射线AM交CB于D;
(2)过点D作DE⊥AB,垂足为E,先证明△ACD≌△AED得到AC=AE,CD=DE=3,再由勾股定理得求的BE长,然后在Rt△ABC中,设AC=x,则AB=AE+BE=x+4,最后再次运用勾股定理求解即可.
解:(1)如图:
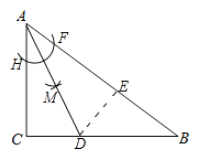
(2)过点D作DE⊥AB,垂足为E.则∠AED=∠BED=90°
∵AD平分∠BAC
∴CD=DE
在RtACD和RtAED中
CD=DE,AD=AD
∴ △CDE≌△AED(HL)
∴AC=AE,CD=DE=3
在Rt△BDE中,
由勾股定理得:DE2+BE2=BD2
∴BE2=BD2-DE2=52-32=16.
∴BE=4
在Rt△ABC中,设AC=x,则AB=AE+BE=x+4.
由勾股定理得:AC2+BC2=AB2,即x2+82=(x+4)2
解得:x=6,即AC=6.

【题目】为进一步推进青少年毒品预防教育“627“工程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,甘肃省各市高度重视全国青少年禁毒知识竞赛活动,强化措施落实,落实工作责任,取得了一定成绩.某市实验中学针对该校九年级学生的知识竞赛成绩绘制了如下不完整的统计图表.
知识竞赛成绩频数分布表
组别 | 成绩(分数) | 人数 |
A | 95≤x<100 | 300 |
B | 90≤x<95 | a |
C | 85≤x<90 | 150 |
D | 80≤x<85 | 200 |
E | 75≤x<80 | b |
根据所给信息,解答下列问题.
(1 )a=_____,b=_____.
(2)请求出C组所在扇形统计图中的圆心角的度数.
(3)补全知识竞赛成绩频数分布直方图.
(4)已知该市九年级有3500名学生,请估算全市九年级知识竞赛成绩低于80分的人数

【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
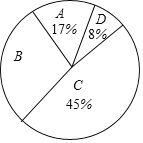
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。