题目内容
（2012•安溪县质检）如图，D、E分别是等边三角形ABC的AB、CA边延长线上的点，且BD=AE，连接BE、CD．求证：BE=CD．分析：由三角形ABC为等边三角形，利用等边三角形的性质得到一对角相等，一对边相等，再由AE=BD，利用SAS得出三角形AEB与三角形BDC全等，利用全等三角形的对应边相等可得出BE=CD，得证．
解答：证明：∵△ABC为等边三角形，
∴∠BAC=∠ABC=60°，AB=BC，
∴∠EAB=∠DBC=120°，
在△AEB和△BDC中，
∵
，
∴△AEB≌△BDC（SAS），
∴BE=CD．
∴∠BAC=∠ABC=60°，AB=BC，
∴∠EAB=∠DBC=120°，
在△AEB和△BDC中，
∵
|
∴△AEB≌△BDC（SAS），
∴BE=CD．
点评：此题考查了全等三角形的判定与性质，以及等边三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
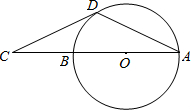（2012•安溪县质检）如图，AB是⊙O的直径，点C在AB的延长线上，CD是⊙O的切线，D为切点，若∠A=25°，则∠C=（ ）
（2012•安溪县质检）若一次函数y=（m-1）x+2的图象如图所示，则m的取值范围是（ ）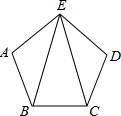
（2012•安溪县质检）如图，正五边形ABCDE中，∠BEC=
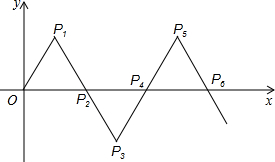点P3（