题目内容
【题目】如图,已知锐角△ABC中,AB、AC边的中垂线交于点O 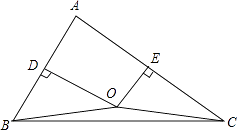
(1)若∠A=α(0°<α<90°),求∠BOC;
(2)试判断∠ABO+∠ACB是否为定值;若是,求出定值,若不是,请说明理由.
【答案】
(1)解:AB、AC边的中垂线交于点O,
∴AO=BO=CO,
∴∠OAB=∠OBA,∠OCA=∠OAC,
∴∠AOB+∠AOC=(180°﹣∠OAB﹣∠OBA)+(180°﹣∠OAC﹣∠OCA),
∴∠AOB+∠AOC=(180°﹣2∠OAB)+(180°﹣2∠OAC)=360°﹣2(∠OAB+∠OAC)=360°﹣2∠A=360°﹣2α,
∴∠BOC=360°﹣(∠AOB+∠AOC)=2α
(2)解:∠ABO+∠ACB为定值,
∵BO=CO,
∴∠OBC=∠OCB,
∵∠OAB=∠OBA,∠OCA=∠OAC,
∴∠OBC= ![]() (180°﹣2∠A)=90°﹣α,
(180°﹣2∠A)=90°﹣α,
∵∠ABO+∠ACB+∠OBC+∠A=180°,
∴∠ABO+∠ACB=180°﹣α﹣(90°﹣α)=90°
【解析】(1)根据线段垂直平分线的性质得到AO=BO=CO,根据等腰三角形的性质得到∠OAB=∠OBA,∠OCA=∠OAC,根据周角定义即可得到结论;(2)根据等腰三角形的性质得到∠OBC=∠OCB,于是得到∠OBC=90°﹣α,根据三角形的内角和即可得到结论.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目